
【题目】如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),与y轴交于点B(0,2),直线y=![]() x-1与y轴交于点C,与x轴交于点D,点P是线段CD上方的抛物线上一动点,过点P作PF垂直x轴于点F,交直线CD于点E,
x-1与y轴交于点C,与x轴交于点D,点P是线段CD上方的抛物线上一动点,过点P作PF垂直x轴于点F,交直线CD于点E,
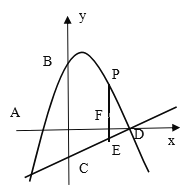
(1)求抛物线的解析式;
(2)设点P的横坐标为m,当线段PE的长取最大值时,解答以下问题.
①求此时m的值.
②设Q是平面直角坐标系内一点,是否存在以P、Q、C、D为顶点的平行四边形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+x+2;(2)①m=![]() ;②存在以P、Q、C、D为顶点的四边形是平行四边形,点Q的坐标为
;②存在以P、Q、C、D为顶点的四边形是平行四边形,点Q的坐标为![]()
【解析】
(1)由题意利用待定系数法,即可求出抛物线的解析式;
(2)①由题意分别用含m的代数式表示出点P,E的纵坐标,再用含m的代数式表示出PE的长,运用函数的思想即可求出其最大值;
②根据题意对以P、Q、C、D为顶点的四边形是平行四边形分三种情况进行讨论与分析求解.
解:(1)将A(﹣1,0),B(0,2)代入y=﹣x2+bx+c,得:
![]() ,解得:b=1,c=2
,解得:b=1,c=2
∴抛物线的解析式为y=﹣x2+x+2.
(2)①∵直线y=![]() x-1与y轴交于点C,与x轴交于点D,
x-1与y轴交于点C,与x轴交于点D,
∴点C的坐标为(0,-1),点D的坐标为(2,0),
∴0<m<2.
∵点P的横坐标为m,
∴点P的坐标为(m,﹣m2+m+2),点E的坐标为(m,![]() m+3),
m+3),
∴PE=﹣m2+m+2﹣(![]() m+3)=﹣m2+
m+3)=﹣m2+![]() m+3=﹣(m﹣
m+3=﹣(m﹣![]() )2+
)2+![]() .
.
∵﹣1<0,0<![]() <2,
<2,
∴当m=![]() 时,PE最长.
时,PE最长.
②由①可知,点P的坐标为(![]() ,
,![]() ).
).
以P、Q、C、D为顶点的四边形是平行四边形分三种情况(如图所示):
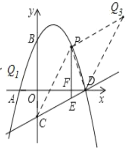
①以PD为对角线,点Q的坐标为![]() ;
;
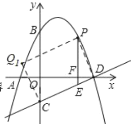
②以PC为对角线,点Q的坐标为![]() ;
;
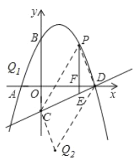
③以CD为对角线,点Q的坐标为![]() .
.
综上所述:在(2)的情况下,存在以P、Q、C、D为顶点的四边形是平行四边形,点Q的坐标为![]() .
.


科目:初中数学 来源: 题型:
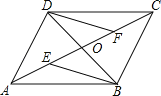
【题目】如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=![]() AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
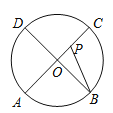
【题目】如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
A. 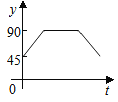 B.
B. 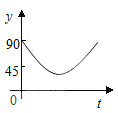 C.
C. 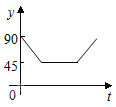 D.
D. 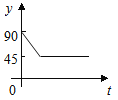
查看答案和解析>>
科目:初中数学 来源: 题型:
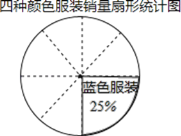
【题目】某超市销售多种颜色的运动服装,其中平均每天销售红、黄、蓝、白四种颜色运动服的数量如表,由此绘制的不完整的扇形统计图如图:
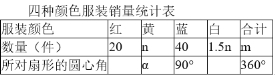
(1)求表中m、n、α的值,并将扇形统计图补充完整:表中m= ,n= ,α= ;
(2)为吸引更多的顾客,超市将上述扇形统计图制成一个可自由转动的转盘,并规定:顾客在本超市购买商品金额达到一定的数目,就获得一次转动转盘的机会.如果转盘停止后,指针指向红色服装区域、黄色服装区域,可分别获得60元、20元的购物券.求顾客每转动一次转盘获得购物券金额的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
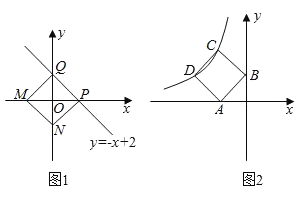
【题目】已知:点M、N分别是x轴y轴上的动点,点P、Q是某个函数图象上的点,当四边形MNPQ为正方形时,称这个正方形为此函数的“梦幻正方形”例如:如图1所示,正方形MNPQ是一次函数y=﹣x+2的其中一个“梦幻正方形”.
(1)若某函数是y=x+5,求它的图象的所有“梦幻正方形”的边长;
(2)若某函数是反比例函数y=![]() (k<0)(如图2所示),它的图象的“梦幻正方形”ABCD,D(﹣4,m)(m<4)在反比例函数图象上,求m的值及反比例函数的解析式.
(k<0)(如图2所示),它的图象的“梦幻正方形”ABCD,D(﹣4,m)(m<4)在反比例函数图象上,求m的值及反比例函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com