
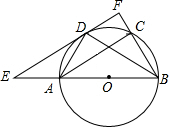
 如图,AB为⊙O的直径,C、D为⊙O上的两点,且D为弧AC的中点,过点D作EF∥AC分别交直线AB,BC于点E、F,AC=6,BD=5.
如图,AB为⊙O的直径,C、D为⊙O上的两点,且D为弧AC的中点,过点D作EF∥AC分别交直线AB,BC于点E、F,AC=6,BD=5.分析 (1)连接半径OD,证明EF⊥OD,可得结论;
(2)由∠DAC=∠DBA,可知:cos∠DAC=cos∠DBA=$\frac{AG}{AD}=\frac{BD}{AB}$,设AD=3x,AB=5x,则BD=4x,可得结果;
(3)计算AB的长,利用勾股定理得BC的长即可.
解答 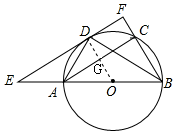 (1)证明:连接OD,
(1)证明:连接OD,
∵D为弧AC的中点,
∴OD⊥AC,
∵EF∥AC,
∴EF⊥OD,
∴EF为⊙O的切线;
(2)∵OD⊥AC
∴AG=CG=$\frac{1}{2}$AC=3,
∵∠DAC=∠DBA,
∴cos∠DAC=cos∠DBA=$\frac{AG}{AD}=\frac{BD}{AB}$,
∴$\frac{AG}{BD}=\frac{AD}{AB}$=$\frac{3}{5}$,
设AD=3x,AB=5x,
∴BD=4x,
∴cos∠DAC=cos∠DBA=$\frac{BD}{AB}=\frac{4x}{5x}$=$\frac{4}{5}$;
(3)由BD=5得:4x=5,
x=$\frac{5}{4}$,
∴AB=5x=5×$\frac{5}{4}$=$\frac{25}{4}$,
在Rt△ACB中,由勾股定理得:BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{(\frac{25}{4})^{2}-{6}^{2}}$=$\frac{7}{4}$.
点评 本题考查了切线的判定、同角三角函数、勾股定理,熟练掌握切线的判定是关键,属于常考题型.


 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
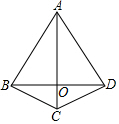 如图,四边形ABCD中,AB=AD,∠ABC=∠ADC.
如图,四边形ABCD中,AB=AD,∠ABC=∠ADC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
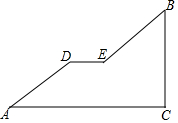 如图是一座人行天桥引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角楼梯AD,BE和一段水平平台DE构成.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图是一座人行天桥引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角楼梯AD,BE和一段水平平台DE构成.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
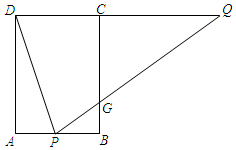 如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com