
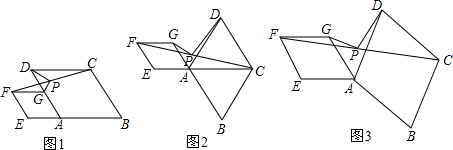
分析 (1)延长GP交CD于H,由菱形的性质得出AB=CD=AD,BE∥CD,AG=FG,FG∥BE,得出FG∥CD,得出内错角相等∠PFG=∠PCH,由ASA证明△PFG≌△PCH,得出FG=CH,PG=PH,证出AG=CH,延长DG=DH,由等腰三角形的三线合一性质得出DP⊥GH,得出∠DPG=90°;求出∠ADC=60°,得出∠PDG=∠PDH=$\frac{1}{2}$∠ADC=30°,由三角函数即可得出$\frac{PG}{PD}$的值;
(2)延长GP交CE于H,连接DH、DG,由菱形的性质得出FG∥EC,得出∠GFP=∠HCP,由ASA证明△PFG≌△PCH,得出FG=CH,PG=PH,证出AG=CH,△ACD是等边三角形,得出AD=CD,得出∠EAG=∠ADC=60°,∠DAC=∠DCA=60°,求出∠GAD=60°,由SAS证明△ADG≌△CDH,得出DG=DH,∠ADG=∠CDH,由等腰三角形的三线合一性质得出DP⊥GH,因此∠DPG=90°,求出∠GDP=30°,由三角函数即可得出$\frac{PG}{PD}$的值;
(3)延长GP到H,使得PH=GP,连接CH、DG、DH,延长DC交EA的延长线于点M,同(2)可证△PFG≌△PCH,得出∠GFC=∠HCF,FG=CH,证出∠GAD=∠DCH,AG=CH,由SAS证明△ADG≌△CDH,得出∠ADG=∠CDH,DG=DH,因此∠GDH=∠ADC=2α,得出∠DPG=90°,∠GDP=$\frac{1}{2}$∠GDH=α,即可得出$\frac{PG}{PD}$=tanα.
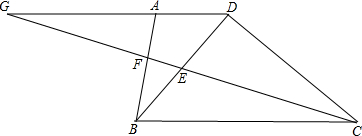
解答 解:(1)延长GP交CD于H,如图1所示: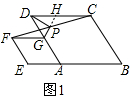
∵在菱形ABCD和菱形AEFG中,
AB=CD=AD,BE∥CD,AG=FG,FG∥BE,
∴FG∥CD,
∴∠PFG=∠PCH,
∵P是线段CF的中点,
∴PF=PC,
在△PFG和△PCH中,
$\left\{\begin{array}{l}{∠PFG=∠PCH}&{\;}\\{PF=PC}&{\;}\\{∠FPG=∠CPH}&{\;}\end{array}\right.$,
∴△PFG≌△PCH(ASA),
∴FG=CH,PG=PH,
∴AG=CH,
∴DG=DH,
∴DP⊥GH(三线合一),
∴∠DPG=90°;
∵∠BAD=120°,
∴∠ADC=60°,
∴∠PDG=∠PDH=$\frac{1}{2}$∠ADC=30°,
∴$\frac{PG}{PD}$=tan∠PDG=tan30°=$\frac{\sqrt{3}}{3}$;
(2)(1)中的两个结论不发生改变;理由如下:
延长GP交CE于H,连接DH、DG,如图2所示: ∵四边形AEFG为菱形,
∵四边形AEFG为菱形,
∴FG∥EC,
∴∠GFP=∠HCP,
∵P是线段CF的中点,
∴PF=PC,
在△PFG和△PCH中,
$\left\{\begin{array}{l}{∠GFP=∠HCP}&{\;}\\{PF=PC}&{\;}\\{∠FPG=∠CPH}&{\;}\end{array}\right.$,
∴△PFG≌△PCH(ASA),
∴FG=CH,PG=PH,
∵FG=AG,
∴AG=CH,
∵四边形ABCD是菱形,
∴AC=CD,
∵∠BAD=∠AEF=120°,
∴∠ACD=60°,
∴△ACD是等边三角形,
∴AD=CD,
∴∠EAG=∠ADC=60°,∠DAC=∠DCA=60°,
∴∠GAD=180°-∠EAG-∠DAC=60°,
在△ADG和△CDH中,
$\left\{\begin{array}{l}{AD=CD}&{\;}\\{∠GAD=∠DCH}&{\;}\\{AG=CH}&{\;}\end{array}\right.$,
∴△ADG≌△CDH(SAS),
∴DG=DH,∠ADG=∠CDH,
∴DP⊥GH,
∴∠DPG=90°,∠GDH=∠ADC=60°,
∴∠GDP=30°,
∴$\frac{PG}{PD}$=tan30°=$\frac{\sqrt{3}}{3}$;
(3)延长GP到H,使得PH=GP,连接CH、DG、DH,延长DC交EA的延长线于点M,如图3所示: 同(2)可证△PFG≌△PCH,
同(2)可证△PFG≌△PCH,
∴∠GFC=∠HCF,FG=CH,
∴FG∥CH,
∵FG∥AE,
∴CH∥EM,
∴∠DCH=∠M,
∵CD∥AB,
∴∠M=∠MAB,
∴∠DCH=∠MAB,
∵∠BAD=∠AEF=180°-2α,
∴∠EAG=∠ADC=2α,
∴∠GAM=180°-2α,
∴∠GAD=∠BAM,
∴∠GAD=∠DCH,
∵AG=FG,
∴AG=CH,
在△ADG和△CDH中,
$\left\{\begin{array}{l}{AD=CD}&{\;}\\{∠GAD=∠DCH}&{\;}\\{AG=CH}&{\;}\end{array}\right.$,
∴△ADG≌△CDH(SAS),
∴∠ADG=∠CDH,DG=DH,
∴∠GDH=∠ADC=2α,
∴∠DPG=90°,∠GDP=$\frac{1}{2}$∠GDH=α,
∴$\frac{PG}{PD}$=tanα.
点评 本题是几何变换综合题目,考查了菱形的性质、全等三角形的判定与性质、等腰三角形的性质、三角函数、等边三角形的判定与性质等知识;本题综合性强,难度较大,需要通过作辅助线,并且需要多次证明三角形全等才能得出结果.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源:2016-2017学年吉林省七年级下学期期中数学模拟试卷(四)(解析版) 题型:填空题
把多项式﹣16x3+40x2y提出一个公因式﹣8x2后,另一个因式是__.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
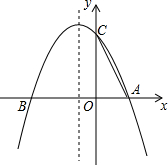 如图,已知抛物线y=ax2+bx+c与x轴交于A(m,0),B(n,0),点A位于点B的右侧,且m,n是一元二次方程x2+2x-3=0的两个根,与y轴交于C(0,3).在抛物线上的对称轴上是否存在点P,使得△PAC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
如图,已知抛物线y=ax2+bx+c与x轴交于A(m,0),B(n,0),点A位于点B的右侧,且m,n是一元二次方程x2+2x-3=0的两个根,与y轴交于C(0,3).在抛物线上的对称轴上是否存在点P,使得△PAC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | 0 | 0.5 | 1 | 1.1 | 1.2 | 1.3 |
| x2+px+q | -15 | -8.75 | -2 | -0.59 | 0.84 | 2.29 |
| A. | 0.5<x<1 | B. | 1<x<1.1 | C. | 1.1<x<1.2 | D. | 1.2<x<1.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
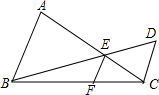 如图,AB∥CD,AC、BD交于点E,EF∥CD交BC于F.求证:
如图,AB∥CD,AC、BD交于点E,EF∥CD交BC于F.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com