
分析 (1)4名学生中女生1名,求出所求概率即可;
(2)列表得出所有等可能的情况数,找出同为男生的情况数,即可求出所求概率.
解答 解:(1)如果随机抽取1名同学单独展示,那么女生展示的概率为$\frac{1}{4}$,
故答案为:$\frac{1}{4}$;
(2)列表如下:
| 男 | 男 | 男 | 女 | |
| 男 | --- | (男,男) | (男,男) | (女,男) |
| 男 | (男,男) | --- | (男,男) | (女,男) |
| 男 | (男,男) | (男,男) | --- | (女,男) |
| 女 | (男,女) | (男,女) | (男,女) | --- |
点评 此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如果实数a,b在数轴上如图所示,化简$\sqrt{{{(2-a)}^2}}-\sqrt{{{(a-3)}^2}}$的结果为( )
如果实数a,b在数轴上如图所示,化简$\sqrt{{{(2-a)}^2}}-\sqrt{{{(a-3)}^2}}$的结果为( )| A. | 5 | B. | 1 | C. | -2a+5 | D. | 2a-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠DOB是∠EOD的两倍,即∠DOB=2∠EOD,求∠AOC,∠COB的度数.
如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠DOB是∠EOD的两倍,即∠DOB=2∠EOD,求∠AOC,∠COB的度数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
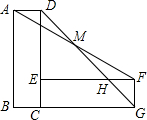 如图所示,长方形ABCD绕点C顺时针旋转90°后得到长方形CEFG,连接DG交EF于H连接AF交DG于点M,若AB=4,BC=1,则AM=$\frac{\sqrt{34}}{2}$.
如图所示,长方形ABCD绕点C顺时针旋转90°后得到长方形CEFG,连接DG交EF于H连接AF交DG于点M,若AB=4,BC=1,则AM=$\frac{\sqrt{34}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com