
【题目】如图:AD是正△ABC的高,O是AD上一点,⊙O经过点D,分别交AB、AC于E、F
(1)求∠EDF的度数;
(2)若AD=6![]() ,求△AEF的周长;
,求△AEF的周长;
(3)设EF、AD相较于N,若AE=3,EF=7,求DN的长.
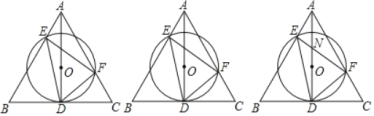
【答案】(1)60°;⑵18;⑶DN=![]()
【解析】
(1)作OI⊥AB于I,OJ⊥AC于J,连接OE,OF,可得△OIE≌△OJF(HL),∠EOF=120°,
可得∠EDF的度数;
(2)设AD与圆O交于点G,连接FG,AD是正△ABC的高,∠B=∠C=60°,CD=BD, GD是圆O的直径,由圆与正三角形的对称性,可得∠BED=∠ FED, 作DK⊥AB,DL⊥AC,DM⊥EF,可得DK=DL,可得△EKD≌EFD与△DMF≌△DLF,可得△AEF的周长=AF+AE+EF=2AL,可得答案.
(3)过E点AC的垂线,长为![]() ,过E点做AD的垂线,长为
,过E点做AD的垂线,长为![]() ,过F做AD的垂线,长为
,过F做AD的垂线,长为![]() ,设AC=x,
,设AC=x,![]() =
=![]() =
=![]() ,AF=
,AF=![]() -10,FC=10-
-10,FC=10-![]() ,EB=x-3,BD=DC=
,EB=x-3,BD=DC=![]() ,由△FDC∽△DEB,可得
,由△FDC∽△DEB,可得![]() ,代入可得x的值,由
,代入可得x的值,由![]() =
=![]() ,可得AN,可求得DN.
,可得AN,可求得DN.
解:(1)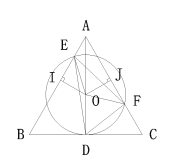
AD是正△ABC的高,∴∠BAC=60°,AD平分∠BAC,
∴∠BAD=∠CAD=30°,
作OI⊥AB于I,OJ⊥AC于J,连接OE,OF,∴OI=OJ,
∴△OIE≌△OJF(HL),∴∠IOE=∠JOF
∴∠EOF=∠EOJ+∠FOJ=∠EOJ+∠IOE=∠IOJ=120°,
∴∠EDF=![]() ∠EOF=60°
∠EOF=60°
⑵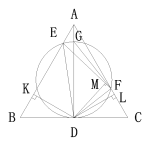
设AD与圆O交于点G,连接FG,AD是正△ABC的高,∠B=∠C=60°,CD=BD, GD是圆O的直径,由圆与正三角形的对称性,可得∠BED=∠ FED, 作DK⊥AB,DL⊥AC,DM⊥EF,可得DK=DL
![]() ∠BED=∠ FED,DK⊥AB, DM⊥EF,ED=ED
∠BED=∠ FED,DK⊥AB, DM⊥EF,ED=ED
![]() △EKD≌EFD,
△EKD≌EFD, ![]() EK=EM,DK=DM,
EK=EM,DK=DM,
在△DMF与△DLF中,
DK=DM=DL, DL⊥AC,DM⊥EF,
![]() △DMF≌△DLF,
△DMF≌△DLF, ![]() MF=FL
MF=FL
易得:AK=AL,AL=![]() AC=9
AC=9
△AEF的周长=AF+AE+EF=2AL,AL=9,∴![]() =18=
=18=![]()
⑶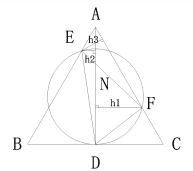
过E点AC的垂线,长为![]() ,过E点做AD的垂线,长为
,过E点做AD的垂线,长为![]() ,过F做AD的垂线,长为
,过F做AD的垂线,长为![]() ,
,
设AC=x,![]() =
=![]() =
=![]() ,AF=
,AF=![]() -10,FC=10-
-10,FC=10-![]() ,EB=x-3,BD=DC=
,EB=x-3,BD=DC=![]() ,
,
由△FDC∽△DEB,可得![]() ,代入得:
,代入得:
![]() ,解得:
,解得:![]() =12,
=12,![]() =
=![]() (舍去),
(舍去),
AF=![]() -10=8,AD=
-10=8,AD=![]() =
=![]() ,
,
![]() =
=![]()
可得AN=![]()
![]() DN=
DN=![]()


科目:初中数学 来源: 题型:
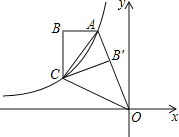
【题目】如图,双曲线y=![]() (x<0)经过Rt△ABC的两个顶点A,C,∠ABC=90°,AB∥x轴,连接OA,将Rt△ABC沿AC翻折后得到Rt△AB′C,点B′刚好落在线段OA上,连接OC,OC恰好平分OA与x轴负半轴的夹角,若Rt△ABC的面积为2,则k的值为___.
(x<0)经过Rt△ABC的两个顶点A,C,∠ABC=90°,AB∥x轴,连接OA,将Rt△ABC沿AC翻折后得到Rt△AB′C,点B′刚好落在线段OA上,连接OC,OC恰好平分OA与x轴负半轴的夹角,若Rt△ABC的面积为2,则k的值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,将对角线AC绕对角线交点O旋转,分别交边AD、BC于点E、F,点P是边DC上的一个动点,且保持DP=AE,连接PE、PF,设AE=x(0<x<3).
(1)填空:PC= ,FC= ;(用含x的代数式表示)
(2)求△PEF面积的最小值;
(3)在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了以“责任、感恩”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图,

(1)该班有 人,学生选择“和谐”观点的有 人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 度;
(2)如果该校有360名初三学生,利用样本估计选择“感恩”观点的初三学生约有 人;
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在推进城乡义务教育均衡发展工作中,我市某区政府通过公开招标的方式为辖区内全部乡镇中学采购了某型号的学生用电脑和教师用笔记本电脑,其中,A乡镇中学更新学生用电脑110台和教师用笔记本电脑32台,共花费30.5万元;B乡镇中学更新学生电脑55台和教师用笔记本电脑24台,共花费17.65万元.
(1)求该型号的学生用电脑和教师用笔记本电脑单价分别是多少万元?
(2)经统计,全部乡镇中学需要购进的教师用笔记本电脑台数比购进的学生用电脑台数的![]() 少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
少90台,在两种电脑的总费用不超过预算438万元的情况下,至多能购进的学生用电脑和教师用笔记本电脑各多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.

(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
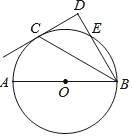
【题目】如图,点C在以AB为直径的⊙O上,BD与过点C的切线垂直于点D,BD与⊙O交于点E.
(1)求证:BC平分∠DBA;
(2)连接AE和AC,若cos∠ABD=![]() ,OA=m,请写出求四边形AEDC面积的思路.
,OA=m,请写出求四边形AEDC面积的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() 下列结论中:
下列结论中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有两个不相等的实数根;
有两个不相等的实数根;![]() 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为![]() ;
;![]() 若点
若点![]() 在该抛物线上,则
在该抛物线上,则![]() .
.
其中正确的有![]()
![]()
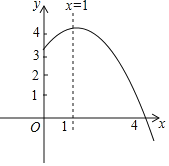
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:

(1)请将下表补充完整:

(2)请从下列三个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com