
【题目】下列各组数据中能作为直角三角形的三边长的是( )
A.![]() ,
, ![]() ,
, ![]()
B.1,1, ![]()
C.4,5,6
D.1, ![]() ,2
,2
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】【知识链接】 有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.
例如: ![]() 的有理化因式是
的有理化因式是 ![]() ;1﹣
;1﹣ ![]() 的有理化因式是1+
的有理化因式是1+ ![]() .
.
分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到化去分母中根号的目的.如:![]() =
= ![]() =
= ![]() ﹣1,
﹣1, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() .
.
(1)【知识理解】 填空:2 ![]() 的有理化因式是;
的有理化因式是;
直接写出下列各式分母有理化的结果:
① ![]() =;②
=;② ![]() = .
= .
(2)【启发运用】 计算: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个图形和它经过平移所得的图形中,两组对应点所连的线段的关系是( )
A.平行B.相等
C.平行(或在同一条直线上)且相等D.既不平行,又不相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:

(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船以16海里/时的速度离开港口(如图),向北偏东40°方向航行,另一艘轮船在同时以12海里/时的速度向北偏西一定的角度的航向行驶,已知它们离港口一个半小时后相距30海里(即BA=30),问另一艘轮船的航行的方向是北偏西多少度?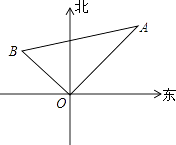
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com