
分析 (1)可根据“改造一所A类学校和两所B类学校共需资金230万元;改造两所A类学校和一所B类学校共需资金205万元”,列出方程组求出答案;
(2)根据“共需资金1575万元”“A类学校不超过6所”,进行判断即可.
解答 解:(1)设改造一所A类学校和一所B类学校所需的改造资金分别为a万元和b万元.
依题意得:$\left\{\begin{array}{l}{a+2b=230}\\{2a+b=205}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=60}\\{b=85}\end{array}\right.$.
答:改造一所A类学校和一所B类学校所需的改造资金分别为60万元和85万元;
(2)设该县有A、B两类学校分别为m所和n所.
则60m+85n=1575,
解得 m=-$\frac{17}{12}$,
∵A类学校不超过6所,
∴-$\frac{17}{12}$n+$\frac{315}{12}$≤6,
∴n≥14.3,
即B类学校至少有15所.
点评 本题考查了不等式的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系:
(1)“改造一所A类学校和两所B类学校共需资金230万元;改造两所A类学校和一所B类学校共需资金205万元”;
(2)“共需资金1575万元”“A类学校不超过6所”.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
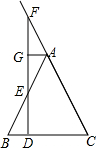 如图,在△ABC中,AB=AC,D是底边BC上的一个动点,过点D作BC的垂线分别交一腰和另一腰的延长线于点E、F,过点A作AG⊥DF于点G.求证:AE=AF.
如图,在△ABC中,AB=AC,D是底边BC上的一个动点,过点D作BC的垂线分别交一腰和另一腰的延长线于点E、F,过点A作AG⊥DF于点G.求证:AE=AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
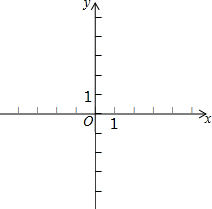 已知一次函数y=2x+1,请你在给出的坐标系中画出它的图象,并根据它的图象回答下列问题:
已知一次函数y=2x+1,请你在给出的坐标系中画出它的图象,并根据它的图象回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com