
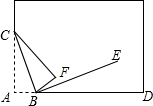
 如图,将长方形纸片的一角折叠,使顶点A落在F处,折痕为BC.
如图,将长方形纸片的一角折叠,使顶点A落在F处,折痕为BC.分析 (1)根据翻折的性质可知△ABC≌△FBC,从而得出∠ABC=∠FBC;
(2)由翻折的性质可知∠FBC=∠ABC=$\frac{1}{2}$∠ABF,根据BE是∠FBD的平分线,利用角平分线的定义可得出∠FBE=$\frac{1}{2}$∠FBD,将∠FBC和∠FBE相加结合∠ABF与∠FBD互补即可得出∠CBE=90°,由此即可得出BE⊥BC;
(3)设∠FBE=x°,根据翻折的性质结合角平分线的定义即可得出∠ABC=∠FBC=2x°、∠DBE=∠FBE=x°,再根据∠ABC+∠FBC+∠FBE+∠DBE=180°即可得出关于x的一元一次方程,解之即可得出结论.
解答 解:(1)根据翻折的性质可知:△ABC≌△FBC,
∴∠ABC=∠FBC.
故答案为:=.
(2)BE⊥BC,理由如下:
∵∠FBC由∠ABC翻折而成,
∴∠FBC=∠ABC=$\frac{1}{2}$∠ABF.
∵BE是∠FBD的平分线,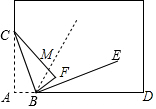
∴∠FBE=$\frac{1}{2}$∠FBD,
∴∠CBE=∠FBC+∠FBE=$\frac{1}{2}$∠ABF+$\frac{1}{2}$∠FBD=$\frac{1}{2}$(∠ABF+∠FBD)=$\frac{1}{2}$×180°=90°.
∴BE⊥BC.
(3)依照题意画出图形,如图所示.
设∠FBE=x°,
∵BE是∠FBD的平分线,
∴∠DBE=∠FBE=x°.
∵∠FBM由∠FBE翻折而成,
∴∠FBM=∠FBE=x°.
∵BM平分∠FBC,
∴∠FBC=2∠FBM=2x°,
∴∠ABC=∠FBC=2x°.
∵∠ABC+∠FBC+∠FBE+∠DBE=180°,
∴2x+2x+x+x=6x=180,
∴x=30.
∴∠FBE=30°.
点评 本题考查了角的计算、翻折变换、角平分线的定义以及解一元一次方程,解题的关键是:(1)熟练掌握翻折的特性;(2)通过角的计算求出∠CBE=90°;(3)根据角的关系找出关于x的一元一次方程.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
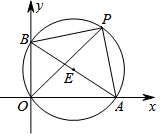 如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )
如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )| A. | $\sqrt{6}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{6}+\sqrt{2}$ | D. | $1+\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 将l1向左平移1个单位 | B. | 将l1向右平移1个单位 | ||
| C. | 将l1向上平移2个单位 | D. | 将l1向上平移1个单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
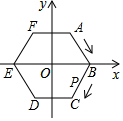 如图,在平面直角坐标系中,六边形ABCDEF是半径为1的正六边形,点O为正六边形ABCDEF的中心,点P从点B出发,沿正六边形按顺时针方向运动,速度为每秒1个单位长度,则第2017秒时,点P的坐标是( )
如图,在平面直角坐标系中,六边形ABCDEF是半径为1的正六边形,点O为正六边形ABCDEF的中心,点P从点B出发,沿正六边形按顺时针方向运动,速度为每秒1个单位长度,则第2017秒时,点P的坐标是( )| A. | ($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) | B. | (-1,0) | C. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) | D. | ($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线a∥b,直线c与直线a、b分别相交于点A、B,AD⊥b,垂足为D,若∠1=37°,则∠2=( )
如图,直线a∥b,直线c与直线a、b分别相交于点A、B,AD⊥b,垂足为D,若∠1=37°,则∠2=( )| A. | 53° | B. | 63° | C. | 37° | D. | 67° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com