
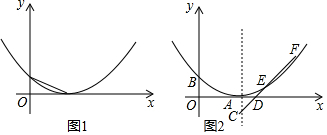
分析 (1)由题意A(h,0),B(0,$\frac{1}{4}$h2),根据OA=2OB,列出方程即可解决问题.
(2)如图1中,MN=4AB,MN∥AB,作MG⊥x轴于G.由△AOB∽△NGM,可得$\frac{OB}{MG}$=$\frac{OA}{GN}$=$\frac{AB}{MN}$=$\frac{1}{4}$,由OA=2.OB=1,推出MG=4,GN=8,推出点M的纵坐标为4,y=4时,4=$\frac{1}{4}$(x-2)2,解得x=-2或6,推出M(-2,4)或(6,4),G(-2,0)或(6,0),推出N(6,0)或(14,0),由此即可解决问题.
(3)如图2中,是定值.以点C为原点作新的坐标系,设抛物线的解析式为y′=$\frac{1}{4}$x′2+m,设直线CD的解析式为y′=kx′,E(x′1,y′1),F(x′2,y′2),作FK⊥AC于K,EH⊥CA于H,
易知$\frac{CD}{CE}$=$\frac{CA}{CH}$=$\frac{CA}{y{′}_{1}}$,$\frac{CD}{CF}$=$\frac{CA}{CK}$=$\frac{CA}{y{′}_{2}}$,推出$\frac{CD}{CE}$+$\frac{CD}{CF}$=CA•$\frac{y{′}_{1}+y{′}_{2}}{y{′}_{1}y{′}_{2}}$,求出y′1+y′2,y′1•y′2,代入即可解决问题.
解答 解:(1)由题意A(h,0),B(0,$\frac{1}{4}$h2),
∴OA=h,OB=$\frac{1}{4}$h2,
∵OA=2OB,
∴h=2×$\frac{1}{4}$h2,
∴h=2或0(舍弃),
∴h=2.
(2)如图1中,MN=4AB,MN∥AB,作MG⊥x轴于G.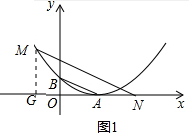
∵△AOB∽△NGM,
∴$\frac{OB}{MG}$=$\frac{OA}{GN}$=$\frac{AB}{MN}$=$\frac{1}{4}$,
∵OA=2.OB=1,
∴MG=4,GN=8,
∴点M的纵坐标为4,y=4时,4=$\frac{1}{4}$(x-2)2,
解得x=-2或6,
∴M(-2,4)或(6,4),∴G(-2,0)或(6,0),
∴N(6,0)或(14,0),
∴△MON的面积=$\frac{1}{2}$×6×4=12或$\frac{1}{2}$×14×4=28,
∴△MNO的面积为12或28.
(3)如图2中,$\frac{CD}{CE}$+$\frac{CD}{CF}$的值是定值.理由如下: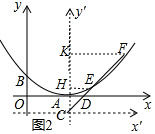
以点C为原点作新的坐标系,设抛物线的解析式为y′=$\frac{1}{4}$x′2+m,设直线CD的解析式为y′=kx′,E(x′1,y′1),F(x′2,y′2),
作FK⊥AC于K,EH⊥CA于H,
易知$\frac{CD}{CE}$=$\frac{CA}{CH}$=$\frac{CA}{y{′}_{1}}$,$\frac{CD}{CF}$=$\frac{CA}{CK}$=$\frac{CA}{y{′}_{2}}$,
∴$\frac{CD}{CE}$+$\frac{CD}{CF}$=CA•$\frac{y{′}_{1}+y{′}_{2}}{y{′}_{1}y{′}_{2}}$,
由$\left\{\begin{array}{l}{y′=kx′}\\{y′=\frac{1}{4}{x′}^{2}+m}\end{array}\right.$消去y′得到x′2-4kx′+m=0,
∴x′1+x′2=4k,x′1•x′2=m,可得y′1+y′2=4k2,y′1•y′2=k2m,
∴$\frac{CD}{CE}$+$\frac{CD}{CF}$=CA•$\frac{y{′}_{1}+y{′}_{2}}{y{′}_{1}y{′}_{2}}$=m•$\frac{4{k}^{2}}{{k}^{2}m}$=4,是定值.
点评 本题考查二次函数综合题、一次函数的应用、相似三角形的判定和性质、平行线的性质等知识,解题的关键是灵活运用待定系数法确定点的坐标,学会构建新的平面直角坐标系解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | m4•m5=m9 | B. | 5x-7x=-2x | ||
| C. | (-x)5÷(-x)2=-x3 | D. | $\frac{{a}^{2}+4a+4}{-{a}^{2}+4}$=$\frac{a+2}{a-2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
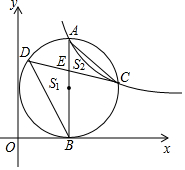 如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.
如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 应试者 | 听 | 说 | 读 | 写 |
| 甲 | 85 | 78 | 85 | 73 |
| 乙 | 73 | 80 | 82 | 83 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 累计购物 | 130 | 250 | … |
| 在甲商场 实际花费 | 100+(130-100)×90% | 100+(250-100)×90% | … |
| 在乙商场 实际花费 | 50+(130-50)×95% | 50+(250-50)×95% | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
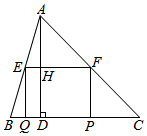 如图,在锐角△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
如图,在锐角△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
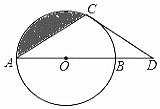 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,⊙O的半径为3,$\widehat{BC}$的长为π.
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,⊙O的半径为3,$\widehat{BC}$的长为π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com