
【题目】如图,在Rt△ABC中,∠C=90°,O是AB上一点,⊙O与BC相切于点E,交AB于点F,连接AE,若AF=2BF,则∠CAE的度数是 . 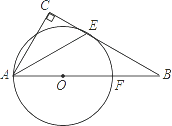
【答案】30°
【解析】解:连接OE、EF,
∵⊙O与BC相切于点E,
∴OE⊥BC,
∵AF是直径,
∴∠AEF=90°,
∵OA=OF= ![]() AF,AF=2BF,
AF,AF=2BF,
∴OF=BF,
∴OE=OF=EF,
∴∠OEF=60°,
∴∠AEO=90°﹣60°=30°,
∵AC⊥BC,OE⊥BC,
∴OE∥AC,
∴∠CAE=∠AEO=30°,
所以答案是30°.
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质),还要掌握圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,一架飞机由A向B沿水平直线方向飞行,在航线AB的正下方有两个山头C、D.飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°.飞机飞行了6千米到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.求山头C、D之间的距离.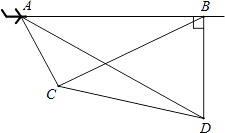
查看答案和解析>>
科目:初中数学 来源: 题型:
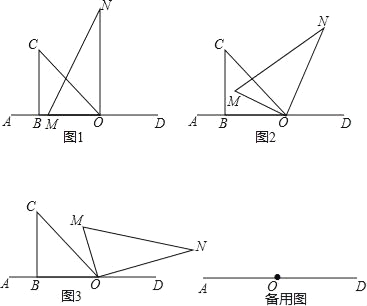
【题目】将一副直角三角板按如图1 摆放在直线AD 上(直角三角板OBC 和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC 不动,将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒.
(1)如图2,当t= 秒时,OM 平分∠AOC,此时∠NOC﹣∠AOM= ;
(2)继续旋转三角板MON,如图3,使得OM、ON 同时在直线OC 的右侧,猜想∠NOC与∠AOM 有怎样的数量关系?并说明理由(数量关系中不能含t);
(3)直线AD 的位置不变,若在三角板MON 开始顺时针旋转的同时,另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转,当OM 旋转至射线OD 上时,两个三角板同时停止运动.
①当t= 秒时,∠MOC=15°;
②请直接写出在旋转过程中,∠NOC 与∠AOM 的数量关系(数量关系中不能含t).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以4cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以3cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了 s时,以C点为圆心,2cm为半径的圆与直线EF相切.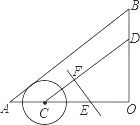
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级学生小聪和小明完成了数学实验《钟面上的数学》之后,自制了一个模拟钟面,如图所示,O为模拟钟面圆心,M、O、N在一条直线上,指针OA、OB分别从OM、ON出发绕点O转动,OA运动速度为每秒15°,OB运动速度为每秒5°,当一根指针与起始位置重合时,运动停止,设转动的时间为t秒,请你试着解决他们提出的下列问题:
(1)若OA顺时针转动,OB逆时针转动,t= 秒时,OA与OB第一次重合;
(2)若它们同时顺时针转动,
①当 t=2秒时,∠AOB= °;
②当t为何值时,OA与OB第一次重合?
③当t为何值时,∠AOB=30°?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下内容:
已知实数m,n满足m+n=5,且![]() 求k的值,
求k的值,
三位同学分别提出了以下三种不同的解题思路:
甲同学:先解关于m,n的方程组![]() ,再求k的值、
,再求k的值、
乙同学:将原方程组中的两个方程相加,再求k的值
丙同学:先解方程组![]() ,再求k的值
,再求k的值
(1)试选择其中一名同学的思路,解答此题
(2)试说明在关于x、y的方程组![]() 中,不论a取什么实数,x+y的值始终不变。
中,不论a取什么实数,x+y的值始终不变。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com