
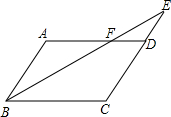
 如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,且AF=2FD.
如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,且AF=2FD.分析 (1)根据平行四边形对角相等可得∠A=∠C,对边平行可得AB∥CD,根据两直线平行,内错角相等得到∠ABF=∠E,然后利用两角对应相等,两三角形相似即可证明.
(2)由于△BCE∽△FDE,可根据两三角形的相似比,求出△FDE的面积,也就求出了四边形BCDF的面积.同理可根据△DEF∽△AFB,求出△AFB的面积.由此可求出?ABCD的面积.
解答 解:
(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,
∵AB∥CD,
∴∠ABF=∠E,
在△ABF和△CEB中,∠A=∠C,∠ABF=∠E,
∴△ABF∽△CEB;
(2)解:∵AF=2FD,
∴AD=3FD,
∵DF:BC=1:3,
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AD=BC,
∴△ABF∽△DEF,△CEB∽△DEF,
∴S△ABF:S△DEF=AF2:FD2,S△BCE:S△FDE=BC2:FD2,
∵△CEB的面积为9,
∴△FDE的面积为1,
∴△ABF的面积为4,
∴?ABCD的面积=9-1+4=12.
点评 本题考查了相似三角形的判定和性质、平行四边形的判定以及三角形的面积,是中考的重点内容,要熟练掌握,熟记平行四边形的各种性质以及相似三角形的各种判断方法是解题的关键.


科目:初中数学 来源: 题型:选择题
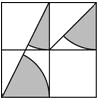 如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )
如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )| A. | $\frac{1}{4}$π | B. | $\frac{3}{4}$π | C. | $\frac{5}{8}$π | D. | $\frac{3}{8}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
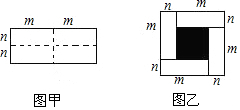 已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com