
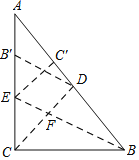
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,沿CD折叠,使点B落在CA边上的B′处,展开后,再沿BE折叠,使点C落在BA边上的C′处,CD与BE交于点F.
(1)求AC′的长度;
(2)求CE的长度;
(3)比较四边形EC′DF与△BCF面积的大小,并说明理由.
【答案】(1)2;(2)![]() ;(3)S四边形EC′DF<S△BCF,理由详见解析.
;(3)S四边形EC′DF<S△BCF,理由详见解析.
【解析】
(1)由勾股定理得出AB的长度,根据翻折可知BC=BC′,即可求AC′的长度;
(2)设CE的长为x,根据翻折可得EC′=EC,则AE=4-x,在Rt△AC′E中根据勾股定理即可求C′E的长度;
(3)过点D分别作DG⊥AC于G,DH⊥BC于H,根据翻折可得CD为∠ACB的角平分线,得出DG=DH,然后由面积法求得DH的长,再求得△BDC和△BEC′的面积,由S△BDC=S△BFC+S△BDF,S△BEC′=S四边形EC′DF+S△BDF,进而可以比较四边形EC′DF与△BCF面积的大小.
解:(1)∵∠ACB=90°,BC=3,AC=4,
∴AB=![]() ,
,
根据翻折可知:BC=BC′=3,
∴AC′=AB﹣BC′=5﹣3=2;
(2)由折叠的性质可得:
∠BC′E=∠BCE=90°=∠AC′E=90°,CE=CE′,
设CE=x,则C′E=x,AE=4-x,
在Rt△AC′E中,由勾股定理得,
x2+22=(4-x)2,解得x=![]() .
.
即CE的长度为![]() ;
;
(3)结论:S四边形EC′DF<S△BCF,理由如下:
过点D分别作DG⊥AC于G,DH⊥BC于H,
由折叠得,CD为∠ACB的角平分线,∴DG=DH,
∵S△ABC=S△ACD+S△BCD,∴![]() ×AC×BC=
×AC×BC=![]() ×AC×DG+
×AC×DG+![]() ×BC×DH,
×BC×DH,
∴3×4=3×DH+4×DH,∴DH=![]() .
.
∴S△BDC=![]() BCDH=
BCDH=![]() 3×
3×![]() =
=![]() ,S△BEC′=S△BEC=
,S△BEC′=S△BEC=![]() BCCE=
BCCE=![]() ×3×
×3×![]() =
=![]() ,
,
∵![]() >
>![]() ,∴S△BDC>S△BEC′,
,∴S△BDC>S△BEC′,
∵S△BDC=S△BFC+S△BDF,S△BEC′=S四边形EC′DF+S△BDF,
∴S四边形EC′DF<S△BCF.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,点E是边BC的中点,AF∥ED,AE∥DF
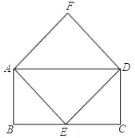
(1)求证:四边形AEDF为菱形;
(2)试探究:当AB:BC= ,菱形AEDF为正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
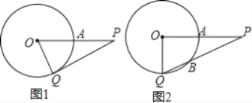
【题目】已知P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
(1)如图1,若PQ是⊙O的切线,求∠QOP的大小;
(2)如图2,若∠QOP=90°,求PQ被⊙O截得的弦QB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的各边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG.

(1)求证:△BDE≌△BAC;
(2)求证:四边形ADEG是平行四边形.
(3)直接回答下面两个问题,不必证明:
①当△ABC满足条件_____________________时,四边形ADEG是矩形.
②当△ABC满足条件_____________________时,四边形ADEG是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识
的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,
并将检查结果绘制成下面两个统计图.
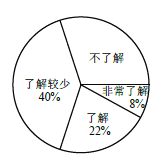
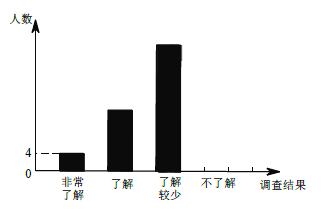
(1)本次调查的学生共有__________人,估计该校1200 名学生中“不了解”的人数是__________人.
(2)“非常了解”的4 人有![]() 两名男生,
两名男生,![]() 两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
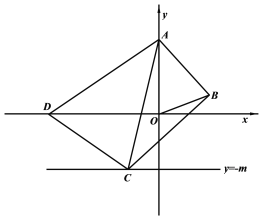
【题目】已知:如图,在平面直角坐标系中,O为坐标原点,△OAB的顶点A、B的坐标分别是A(0,5),B(3,1),过点B画BC⊥AB交直线![]() 于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
(1)求证:△ABC≌△AOD.
(2)设△ACD的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(3)若四边形ABCD恰有一组对边平行,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
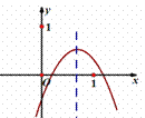
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则在下列代数式:①ac;②a+b+c;③4a-2b+c;④2a+b;⑤b2-4ac中,值大于0的序号为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.
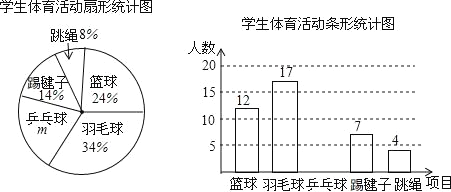
(1)m= %,这次共抽取了 名学生进行调查;并补全条形图;
(2)请你估计该校约有 名学生喜爱打篮球;
(3)现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com