
分析 过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,根据角平分线上的点到角的两边的距离相等可得DE=DF,再根据角平分线AD将△ABC分成面积比为3:5的两部分,且AB>AC,得出S△ABD:S△ACD=($\frac{1}{2}$AB•DE):($\frac{1}{2}$AC•DF)=AB:AC=5:3,然后由△ABC的周长为41cm,CB=17cm,得出AB+AC=24cm,进而求得
AB与AC的值.
解答 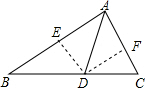 解:如图,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,
解:如图,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,
∵AD是△ABC的角平分线,
∴DE=DF,
∴S△ABD=$\frac{1}{2}$AB•DE,S△ACD=$\frac{1}{2}$AC•DF,
∵AB>AC,
∴S△ABD:S△ACD=($\frac{1}{2}$AB•DE):($\frac{1}{2}$AC•DF)=AB:AC=5:3.
∵△ABC的周长为41cm,CB=17cm,
∴AB+AC=41-17=24,
∴AB=24×$\frac{5}{8}$=15(cm),AC=24×$\frac{3}{8}$=9(cm),
故答案为15,9.
点评 本题主要考查了角平分线上的点到角的两边的距离相等的性质,作出辅助线表示出三角形的面积是解题的关键.


科目:初中数学 来源: 题型:填空题
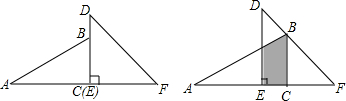
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
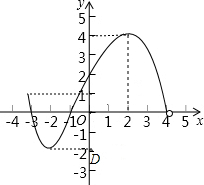 观察图,回答下列问题:
观察图,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A为一次函数y=-x+5与反比例函数y=$\frac{2}{x}$图象的一个交点,AB⊥y轴于点B,AC⊥x轴于点C,则矩形ABOC的面积为多少?周长为多少?
如图,点A为一次函数y=-x+5与反比例函数y=$\frac{2}{x}$图象的一个交点,AB⊥y轴于点B,AC⊥x轴于点C,则矩形ABOC的面积为多少?周长为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | 甲种客车 | 乙种客车 |
| 载客量(人/辆) | 45 | 30 |
| 租金(元/辆) | 1000 | 800 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com