
【题目】我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.
(1)等边三角形“內似线”的条数为 ;
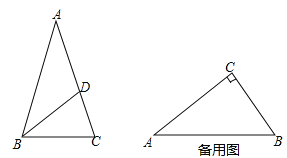
(2)如图,△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求证:BD是△ABC的“內似线”;
(3)在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别在边AC、BC上,且EF是△ABC的“內似线”,求EF的长.
【答案】(1)1;(2)证明见解析;(3)EF的长是![]() .
.
【解析】试题分析:(1)过等边三角形的内心分别作三边的平行线,即可得出答案;
(2)由等腰三角形的性质得出∠ABC=∠C=∠BDC,证出△BCD∽△ABC即可;
(3)分两种情况:①当![]() 时,EF∥AB,由勾股定理求出AB=
时,EF∥AB,由勾股定理求出AB=![]() =5,作DN⊥BC于N,则DN∥AC,DN是Rt△ABC的内切圆半径,求出DN=
=5,作DN⊥BC于N,则DN∥AC,DN是Rt△ABC的内切圆半径,求出DN=![]() (AC+BC-AB)=1,由几啊平分线定理得出
(AC+BC-AB)=1,由几啊平分线定理得出![]() ,求出CE=
,求出CE=![]() ,证明△CEF∽△CAB,得出对应边成比例求出EF=
,证明△CEF∽△CAB,得出对应边成比例求出EF=![]() ;
;
②当![]() 时,同理得:EF=
时,同理得:EF=![]() 即可.
即可.
试题解析:(1)等边三角形“內似线”的条数为3条;理由如下:
过等边三角形的内心分别作三边的平行线,如图1所示:
则△AMN∽△ABC,△CEF∽△CBA,△BGH∽△BAC,
∴MN、EF、GH是等边三角形ABC的內似线”;
(2)∵AB=AC,BD=BC,
∴∠ABC=∠C=∠BDC,
∴△BCD∽△ABC,
∴BD是△ABC的“內似线”;
(3)设D是△ABC的内心,连接CD,

则CD平分∠ACB,
∵EF是△ABC的“內似线”,
∴△CEF与△ABC相似;
分两种情况:①当![]() 时,EF∥AB,
时,EF∥AB,
∵∠ACB=90°,AC=4,BC=3,
∴AB=![]() =5,
=5,
作DN⊥BC于N,如图2所示:
则DN∥AC,DN是Rt△ABC的内切圆半径,
∴DN=![]() (AC+BC-AB)=1,
(AC+BC-AB)=1,
∵CD平分∠ACB,
∴![]() ,
,
∵DN∥AC,
∴![]() ,即
,即![]() ,
,
∴CE=![]() ,
,
∵EF∥AB,
∴△CEF∽△CAB,
∴![]() ,即
,即 ,
,
解得:EF=![]() ;
;
②当![]() 时,同理得:EF=
时,同理得:EF=![]() ;
;
综上所述,EF的长为![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度向
的速度向![]() 点运动,
点运动,![]() 、
、![]() 两点同时出发,其中一点到达终点时另一点也停止运动.若
两点同时出发,其中一点到达终点时另一点也停止运动.若![]() ,当
,当![]() __
__![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①ac<0,②b﹣2a<0,③b2﹣4ac<0,④a﹣b+c<0,正确的是( )
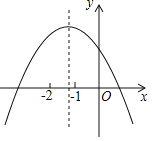
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张仅一面分别标有1,2,3,4的不透明纸片,除所标数字不同外,其余都完全相同.
(1)将四张纸片分成两组,标有1、3的为第一组,标有2、4的为第二组,背面向上,放在桌上,从两组中各随机抽取一张,求两次抽取数字和为5的概率;
(2)将四张纸片洗匀后背面向上,放在桌上,一次性从中随机抽取两张,用树形图法或列表法,求所抽取数字和为5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 为半径的圆恰好经过点
为半径的圆恰好经过点![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]()
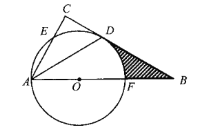
(1)试判断直线![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(2)若![]() ,
,![]() ,求阴影部分的面积(结果保留
,求阴影部分的面积(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
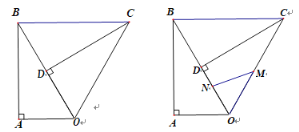
【题目】已知Rt△OAB,OAB90,ABO30,斜边OB4,将Rt△OAB绕点O顺时针旋转60,得到△COD,如图1,连接BC.
(1)求BC的长度;
(2)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿OCB路径匀速运动,N沿OBC路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5个单位/秒,点N的运动速度为1个单位/秒,设运动时间为x秒,△OMN的面积为y,求y关于x的函数解析式,并直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
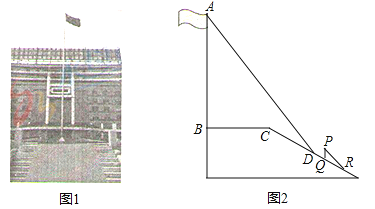
【题目】(2016山东省烟台市)某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下的统计图:
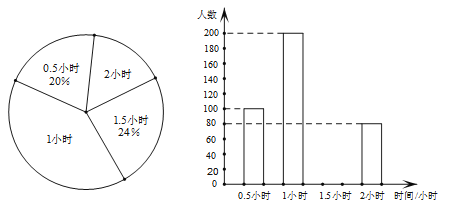
(1)该调查小组抽取的样本容量是多少?
(2)求样本学生中阳光体育运动时间为1.5小时的人数,并补全占频数分布直方图;
(3)请估计该市中小学生一天中阳光体育运动的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OA1B1,△A1A2B2,△A2A3B3,…是分别以A1,A2,A3,…为直角顶点,一条直角边在x轴正半轴上的等腰直角三角形,其斜边的中点C1(x1,y1),C2(x2,y2),C3(x3,y3),…均在反比例函数![]() (x>0)的图象上.则y1+y2+…+y8的值为( )
(x>0)的图象上.则y1+y2+…+y8的值为( )
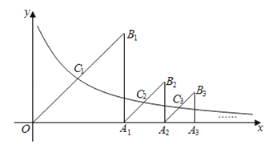
A.![]() B.6C.
B.6C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com