
ЁОЬтФПЁПЃЈЮЪЬтБГОАЃЉНтЗНГЬЃКx4Љ5x2+4=0ЃЎ
етЪЧвЛИівЛдЊЫФДЮЗНГЬЃЌИљОнИУЗНГЬЕФЬиЕуЃЌЮвУЧПЩвдНшжњЁАЛЛдЊЗЈЁБНЋИпДЮЗНГЬЁАНЕДЮЁБЃЌНјЖјНтЕУЮДжЊЪ§ЕФжЕЃЎ
НтЃКЩш x2=yЃЌФЧУД x4=y2ЃЌгкЪЧдЗНГЬПЩБфЮЊ y2Љ5y+4=0ЃЌНтЕУ y1=1ЃЌy2=4ЃЎ ЕБ y1=1 ЪБЃЌx2=1ЃЌx=ЁР1ЃЛЕБ y2=4 ЪБЃЌx2=4ЃЌx=ЁР2ЃЛ
дЗНГЬгаЫФИіИљЃКx1=1ЃЌx2=Љ1ЃЌx3=2ЃЌx4=Љ2ЃЎ
ЃЈДЅРрХдЭЈЃЉВЮееР§ЬтНтЗНГЬЃКЃЈx2+xЃЉ2Љ4ЃЈx2+xЃЉЉ12=0ЃЛ
ЃЈНтОіЮЪЬтЃЉвбжЊЪЕЪ§ xЃЌy ТњзуЃЈ2x+2y+3ЃЉЃЈ2x+2yЉ3ЃЉ=27ЃЌЧѓ x+y ЕФжЕЃЛ
ЃЈЭиеЙЧЈвЦЃЉЗжНтвђЪНЃКЃЈx2+4x+3ЃЉЃЈx2+4x+5ЃЉ+1ЃЎ
ЁОД№АИЁП[ДЅРрХдЭЈ]ЃКx1=Љ3ЃЌx2=2ЃЛ[НтОіЮЪЬт]ЃКx+y=ЁР3ЃЛ[ЭиеЙЧЈвЦ]ЃЈx+2ЃЉ4ЃЎ
ЁОНтЮіЁП
Щшy=x2+xЃЌНЋдЗНГЬзЊЛЏЮЊЙигкyЕФвЛдЊЖўДЮЗНГЬЃЌЭЈЙ§НтЗНГЬЧѓЕУyМДx2+xЕФжЕЃЌШЛКѓдйРДНтЙигкxЕФвЛдЊЖўДЮЗНГЬЃЎ
Щш 2x+2y= aЃЌдђИљОнЦНЗНВюЙЋЪННЋдЗНГЬЛЏЮЊЃКЃЈa+3ЃЉЃЈaЉ3ЃЉ=27ЃЌдйНЋaжЕНјааЧѓНтГ§вд2МДПЩ.
Щш x2+4x+3=aЃЌдђИљОнЦНЗНВюЙЋЪННЋдЗНГЬЛЏЮЊЃК![]() ЃЌдйНЋaжЕДњШыМДПЩЧѓНт.
ЃЌдйНЋaжЕДњШыМДПЩЧѓНт.
[ДЅРрХдЭЈ]ЃК
ЃЈx2+xЃЉ2Љ4ЃЈx2+xЃЉЉ12=0ЃЌ
Щш x2+x=yЃЌдђдЗНГЬЛЏЮЊЃКy2Љ4yЉ12=0ЃЌ НтЕУЃКy1=6ЃЌy2=Љ2ЃЌ
ЕБ y=6 ЪБЃЌx2+x=6ЃЌНтЕУЃКx=Љ3 Лђ 2ЃЛ ЕБ y=Љ2 ЪБЃЌx2+x=Љ2ЃЌ
x2+x+2=0ЃЌ
ЁпДЫЗНГЬжаЕФЁї=12Љ4ЁС1ЁС2=Љ7ЃМ0ЃЌ
ЁрДЫЗНГЬЮоНтЃЛ
ЫљвддЗНГЬЕФНтЮЊЃКx1=Љ3ЃЌx2=2ЃЛ
[НтОіЮЪЬт]ЃК
ЃЈ2x+2y+3ЃЉЃЈ2x+2yЉ3ЃЉ=27ЃЌ
Щш 2x+2y=aЃЌдђдЗНГЬЛЏЮЊЃКЃЈa+3ЃЉЃЈaЉ3ЃЉ=27ЃЌећРэЕУЃКa2=36ЃЌ
НтЕУЃКa=ЁР6ЃЌ МД 2x+2y=ЁР6ЃЌ Ыљвд x+y=ЁР3ЃЛ
[ЭиеЙЧЈвЦ]ЃК Щш x2+4x+3=aЃЌ
дђЃЈx2+4x+3ЃЉЃЈx2+4x+5ЃЉ+1
=aЃЈa+2ЃЉ+1
=a2+2a+1
=ЃЈa+1ЃЉ2
=ЃЈx2+4x+3+1ЃЉ2
=ЃЈx2+4x+4ЃЉ2
=ЃЈx+2ЃЉ4ЃЎ


 ЧЩбЇЧЩСЗЯЕСаД№АИ
ЧЩбЇЧЩСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃК
аЁУїгіЕНвЛИіЮЪЬтЃКдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§БпЕФГЄЗжБ№ЮЊ
Ш§БпЕФГЄЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
аЁУїЪЧетбљНтОіЮЪЬтЕФЃКШчЭМЂйЫљЪОЃЌЯШЛвЛИіе§ЗНаЮЭјИёЃЈУПИіаЁе§ЗНаЮЕФБпГЄЮЊ![]() ЃЉЃЌдйдкЭјИёжаЛГіИёЕу
ЃЉЃЌдйдкЭјИёжаЛГіИёЕу![]() ЃЈМД
ЃЈМД![]() Ш§ИіЖЅЕуЖМдкаЁе§ЗНаЮЕФЖЅЕуДІЃЉЃЌДгЖјНшжњЭјИёОЭФмМЦЫуГі
Ш§ИіЖЅЕуЖМдкаЁе§ЗНаЮЕФЖЅЕуДІЃЉЃЌДгЖјНшжњЭјИёОЭФмМЦЫуГі![]() ЕФУцЛ§ЃЎЫћАбетжжНтОіЮЪЬтЕФЗНЗЈГЦЮЊЙЙЭМЗЈЃЎ
ЕФУцЛ§ЃЎЫћАбетжжНтОіЮЪЬтЕФЗНЗЈГЦЮЊЙЙЭМЗЈЃЎ
ВЮПМаЁУїНтОіЮЪЬтЕФЗНЗЈЃЌЭъГЩЯТСаЮЪЬтЃК
ЃЈ![]() ЃЉЭМ
ЃЉЭМ![]() ЪЧвЛИі
ЪЧвЛИі![]() ЕФе§ЗНаЮЭјИёЃЈУПИіаЁе§ЗНаЮЕФБпГЄЮЊ
ЕФе§ЗНаЮЭјИёЃЈУПИіаЁе§ЗНаЮЕФБпГЄЮЊ![]() ЃЉ ЃЎ
ЃЉ ЃЎ
ЂйРћгУЙЙЭМЗЈдкД№ОэЕФЭМ![]() жаЛГіШ§БпГЄЗжБ№ЮЊ
жаЛГіШ§БпГЄЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФИёЕу
ЕФИёЕу![]() ЃЎ
ЃЎ
ЂкМЦЫуЂйжа![]() ЕФУцЛ§ЮЊ__________ЃЎЃЈжБНгаДГіД№АИЃЉ
ЕФУцЛ§ЮЊ__________ЃЎЃЈжБНгаДГіД№АИЃЉ
ЃЈ![]() ЃЉШчЭМ
ЃЉШчЭМ![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌвд
ЃЌвд![]() ЃЌ
ЃЌ![]() ЮЊБпЯђЭтзїе§ЗНаЮ
ЮЊБпЯђЭтзїе§ЗНаЮ![]() ЃЌ
ЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
ЂйХаЖЯ![]() гы
гы![]() УцЛ§жЎМфЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
УцЛ§жЎМфЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЂкШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌжБНгаДГіСљБпаЮ
ЃЌжБНгаДГіСљБпаЮ![]() ЕФУцЛ§ЮЊ__________ЃЎ
ЕФУцЛ§ЮЊ__________ЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
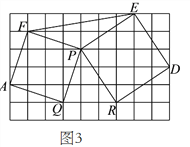
ЁОЬтФПЁПвбжЊЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯDЃН90ЁуЃЌACЦНЗжЁЯBADЃЌЁЯACDЃН30Ёу
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКЁїABCЪЧЕШБпШ§НЧаЮЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕуEдкБпBAЕФбгГЄЯпЩЯЃЌдкБпBCЩЯШЁвЛЕуFЃЌСЌНгECЁЂEFЧвECЃНEFЃЌЧѓжЄЃКBFЃНAEЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНгAFЃЌШЁAFЕФжаЕуGЃЌСЌНгBGВЂбгГЄНЛЯпЖЮECгкMЃЌНЛЯпЖЮADгкRЃЌЙ§ЕуAзіANЁЮECНЛЯпЖЮBRгкNЃЌШєGNЃН2ЃЌEMЃН5ЃЌЧѓCMЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
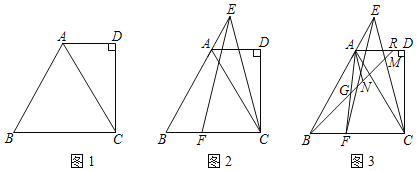
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌABЃН6ЃЌPЪЧACБпЩЯвЛЖЏЕуЃЌгЩAЯђCдЫЖЏЃЈгыAЁЂCВЛжиКЯЃЉЃЌQЪЧCBбгГЄЯпЩЯвЛЖЏЕуЃЌгыЕуPЭЌЪБвдЯрЭЌЕФЫйЖШгЩBЯђCBбгГЄЯпЗНЯђдЫЖЏЃЈQВЛгыBжиКЯЃЉЃЌЙ§PзїPEЁЭABгкEЃЌСЌНгPQНЛABгкDЃЎ
ЃЈ1ЃЉжЄУїЃКдкдЫЖЏЙ§ГЬжаЃЌЕуDЪЧЯпЖЮPQЕФжаЕуЃЛ
ЃЈ2ЃЉЕБЁЯBQDЃН30ЁуЪБЃЌЧѓAPЕФГЄЃЛ
ЃЈ3ЃЉдкдЫЖЏЙ§ГЬжаЯпЖЮEDЕФГЄЪЧЗёЗЂЩњБфЛЏЃПШчЙћВЛБфЃЌЧѓГіЯпЖЮEDЕФГЄЃЛШчЙћБфЛЏЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтЁАбєЙтЬхг§ЁБЛюЖЏЕФПЊеЙЧщПіЃЌДгШЋаЃ2000УћбЇЩњжаЃЌЫцЛњГщШЁВПЗжбЇЩњНјааЮЪОэЕїВщЃЈУПУћбЇЩњжЛФмЬюаДвЛЯюздМКЯВЛЖЕФЛюЖЏЯюФПЃЉЃЌВЂНЋЕїВщНсЙћЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎ

ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБЛЕїВщЕФбЇЩњЙВгаЁЁ ЁЁШЫЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉдкЩШаЮЭГМЦЭМжаЃЌm=ЁЁЃЌn=ЁЁЁЁЁЁЃЌБэЪОЧјгђCЕФдВаФНЧЮЊЁЁЁЁЖШЃЛ
ЃЈ3ЃЉШЋаЃбЇЩњжаЯВЛЖРКЧђЕФШЫЪ§ДѓдМга ЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌ
жаЃЌ![]() жаЕФЕу
жаЕФЕу![]() ЪЧ
ЪЧ![]() БпЩЯЕФвЛЕуЃЌЙ§Еу
БпЩЯЕФвЛЕуЃЌЙ§Еу![]() ЕФЗДБШР§КЏЪ§
ЕФЗДБШР§КЏЪ§![]()
![]() гы
гы![]() БпНЛгкЕу
БпНЛгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() .
.
ЃЈ1ЃЉШчЭМ1ЃЌШєЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЕФУцЛ§ЮЊ5ЃЌЧѓжБЯп
ЕФУцЛ§ЮЊ5ЃЌЧѓжБЯп![]() КЭЗДБШР§КЏЪ§
КЭЗДБШР§КЏЪ§![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
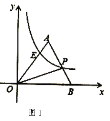
ЃЈ2ЃЉШчЭМ2ЃЌШє![]() ЃЌЙ§
ЃЌЙ§![]() зї
зї![]() ЃЌгы
ЃЌгы![]() НЛгкЕу
НЛгкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌВЂЧв
ЃЌВЂЧв![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓЗДБШР§КЏЪ§
ЃЌЧѓЗДБШР§КЏЪ§![]() ЕФНтЮіЪНМАЕу
ЕФНтЮіЪНМАЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯABCгыЁЯACBЕФЦНЗжЯпНЛгкЕуFЃЌЙ§ЕуFзїDEЁЮBCНЛABгкЕуDЃЌНЛACгкЕуEЃЌФЧУДЯТСаНсТлЃЌЂйЁїBDFЪЧЕШбќШ§НЧаЮЃЛЂкDEЃНBD+CEЃЛЂлШєЁЯAЃН50ЁуЃЌЁЯBFCЃН105ЁуЃЛЂмBFЃНCFЃЎЦфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ
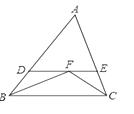
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
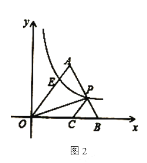
ЁОЬтФПЁПЖЈвхЃКдкЦНУцжБНЧзјБъЯЕжаЃЌЖдгкШЮвтСНЕуA ЃЈaЃЌbЃЉЃЌBЃЈcЃЌdЃЉЃЌШєЕуTЃЈxЃЌyЃЉТњзуxЃН![]() ЃЌyЃН
ЃЌyЃН![]() ЃЌФЧУДГЦЕуTЪЧЕуAКЭBЕФШкКЯЕуЃЎР§ШчЃКMЃЈЉ1ЃЌ8ЃЉЃЌNЃЈ4ЃЌЉ2ЃЉЃЌдђЕуTЃЈ1ЃЌ2ЃЉЪЧЕуMКЭNЕФШкКЯЕуЃЎШчЭМЃЌвбжЊЕуDЃЈ3ЃЌ0ЃЉЃЌЕуEЪЧжБЯпyЃНx+2ЩЯШЮвтвЛЕуЃЌЕуT ЃЈxЃЌyЃЉЪЧЕуDКЭEЕФШкКЯЕуЃЎ
ЃЌФЧУДГЦЕуTЪЧЕуAКЭBЕФШкКЯЕуЃЎР§ШчЃКMЃЈЉ1ЃЌ8ЃЉЃЌNЃЈ4ЃЌЉ2ЃЉЃЌдђЕуTЃЈ1ЃЌ2ЃЉЪЧЕуMКЭNЕФШкКЯЕуЃЎШчЭМЃЌвбжЊЕуDЃЈ3ЃЌ0ЃЉЃЌЕуEЪЧжБЯпyЃНx+2ЩЯШЮвтвЛЕуЃЌЕуT ЃЈxЃЌyЃЉЪЧЕуDКЭEЕФШкКЯЕуЃЎ
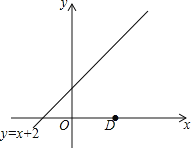
ЃЈ1ЃЉШєЕуEЕФзнзјБъЪЧ6ЃЌдђЕуTЕФзјБъЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧѓЕуT ЃЈxЃЌyЃЉЕФзнзјБъyгыКсзјБъxЕФКЏЪ§ЙиЯЕЪНЃК
ЃЈ3ЃЉШєжБЯпETНЛxжсгкЕуHЃЌЕБЁїDTHЮЊжБНЧШ§НЧаЮЪБЃЌЧѓЕуEЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
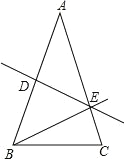
ЁОЬтФПЁПдкЁїABC жаЃЌABЃОBCЃЌABЃНACЃЌDE ЪЧ AB ЕФДЙжБЦНЗжЯпЃЌДЙзуЮЊ DЃЌНЛ AC гк EЃЎ
ЃЈ1ЃЉШєЁЯABEЃН40ЁуЃЌЧѓЁЯEBC ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєЁїABC ЕФжмГЄЮЊ 41cmЃЌвЛБпГЄЮЊ 15cmЃЌЧѓЁїBCE ЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com