
如图8-54,已知在△ABC中,AB=AC=a,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
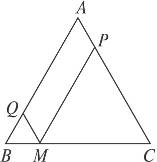
图8-54
(1)求四边形AQMP的周长;
(2)写出图中![]() 的两对相似三角形(不需证明)
的两对相似三角形(不需证明)![]() ;
;
(3)M位于BC的什么位置时,四边形AQMP为菱形?说明你的理由.
2a.
提示:根据平行的性质可以得到平行四边形和两个等腰三角形,由对边和腰相等,四边形的周长等于△ABC的两腰之和.
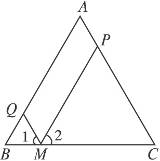
∵PM∥AB,QM∥AC,
∴四边形AQMP为平行四边形,
且∠1=∠C,∠2=∠B.
又∵AB=AC=a,
∴∠B=∠C.
∴∠1=∠B=∠C=∠2.
∴QB=QM,PM=PC.
∴四边形AQMP的周长为
AQ+QM+MP+PA=AQ+QB+PC+PA=AB+AC=2a.
(2)答案:△BQM∽△MPC∽△BAC.
(3)答案:当M为底边BC的中点时,四边形AQMP为菱形.
提示:四边形AQMP已是平行四边形,要使之为菱形,则需有一组邻边相等.
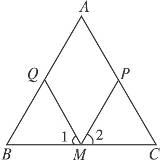
理由:∵M为底边BC的中![]() 点,
点,
∴BM=CM.
由(1)知∠B=∠C,∠1=∠2,
∴△BQM≌△CMP.
∴PM=QM.
由(1)四![]() 边形AQMP为平行四边形,
边形AQMP为平行四边形,
∴四边形AQMP为菱形.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
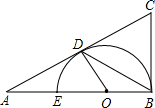 如图,已知在△ABC中,∠B=90°.O是AB上一点,以O为圆心,OB为半径的半圆与AB交于点E,与AC切于点D,AD=2,AE=1.求证:S△AOD、S△BCD是方程10x2-51x+54=0的两个根.
如图,已知在△ABC中,∠B=90°.O是AB上一点,以O为圆心,OB为半径的半圆与AB交于点E,与AC切于点D,AD=2,AE=1.求证:S△AOD、S△BCD是方程10x2-51x+54=0的两个根.查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(湖南怀化卷)数学(解析版) 题型:解答题
如图,已知在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°,
求证:△ABC∽△DEF
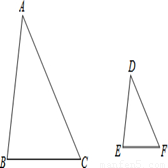
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com