
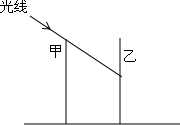
 如图,甲、乙两楼的高都为30m,两楼相距24m,在某一时刻太阳光线与水平线的夹角为30°,则甲楼的影子落在乙楼上的高度为(30-8$\sqrt{3}$)m.
如图,甲、乙两楼的高都为30m,两楼相距24m,在某一时刻太阳光线与水平线的夹角为30°,则甲楼的影子落在乙楼上的高度为(30-8$\sqrt{3}$)m. 分析 过D作甲楼的垂线段DE,得到直角三角形ADE,则∠ADE=30°,DE=BC=24m,在这个三角形中已知一边和一个锐角,满足解直角三角形的条件,可求出AE的长从而求得BD的长.
解答 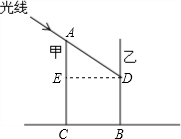 解:如图,过点D作DE⊥AC于E.
解:如图,过点D作DE⊥AC于E.
由题意可知∠ADE=30°,DE=BC=24m.
∵在Rt△ADE中,∠AED=90°,∠ADE=30°,DE=BC=24m,
∴在Rt△ADE中,tan∠ADE=$\frac{AE}{DE}$,
∴AE=DE•tan∠ADE=24•tan30°=8$\sqrt{3}$(m),
则DB=EC=AC-AE=30-8$\sqrt{3}$(m).
故答案为(30-8$\sqrt{3}$).
点评 本题考查了解直角三角形在生活中的实际应用,理清题意,正确的构造直角三角形是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com