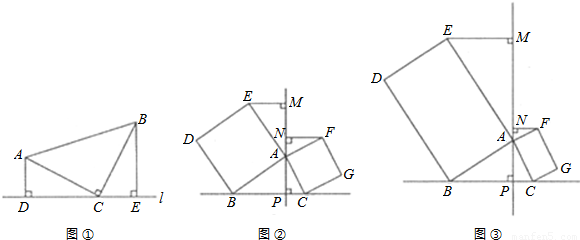
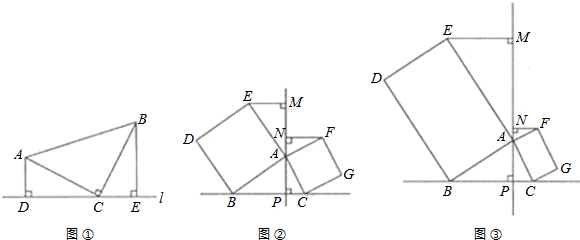
(1)解:∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∴∠ACD=∠CBE.
∵AD⊥DE,BE⊥DE,
∴∠ADE=∠BED=90°,
∴△ADC≌△CEB,
∴AD=CE,DC=BE.
∵DE=DC+CE,
∴DE=BE+AD.
故答案为:DE=BE+AD.
(2)证明:∵四边形ABDE和四边形ACGF都是正方形,
∴AE=AB,∠EAB=90°,
∴∠1+∠2=90°.
∵EM⊥AP,
∴∠1+∠3=90°,
∴∠2=∠3,
∴△EMA≌△APB,
∴EM=AP.
同理可证:△FNA≌△APC,
∴AN=PC.
∵PN=AN+AP,
∴PN=EM+PC.
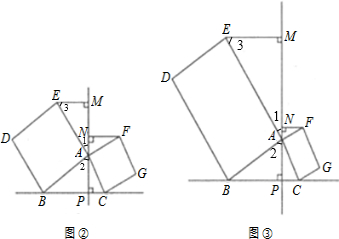
(3)解:结论不成立,有PN=m(EM+PC).
∵四边形ABDE和四边形ACGF是矩形,
∴∠BAE=90°,
∴∠1+∠2=90°.
∵EM⊥AP,
∴∠1+∠3=90°,
∴∠2=∠3,
∴△EMA∽△APB,
∴
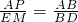
=m,
∴AP=mEM.
同理可得△FNA∽△APC,
∴
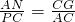
,
∴AN=mPC,
∵PN=PA+NA,
∴PN=m(EM+PC).
分析:(1)利用三角形全等可以得出DC=BE,AD=CE,从而得出线段DE、AD及BE的数量关系.
(2)利用正方形的性质证明△MEA≌△PAB和△FNA≌△APC,从而得出结论PN=EM+PC.
(3)根据三角形相似可以得出PN=m(EM+PC),从而得出结论不成立.
点评:本题考查了相似三角形的判定与性质,全等三角形的判定与性质及正方形的性质的运用.

 (3)解:结论不成立,有PN=m(EM+PC).
(3)解:结论不成立,有PN=m(EM+PC).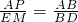 =m,
=m,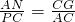 ,
,