
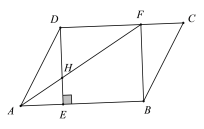
【题目】在平行四边形 ABCD 中,过点 D 作 DE⊥AB 于点 E,点 F 在 CD 上,CF =AE,连接 BF,AF.
(1)求证:四边形 BFDE 是矩形;
(2)若 AF 平分∠BAD,交DE与H点,且 AB=3AE,BF=6,求AH的长.
【答案】(1)证明见解析; (2)4.
【解析】
(1)由CF =AE易得BE=DF.根据有一个角是90度的平行四边形是矩形即可判定.
(2)由AF 平分∠BAD,结合平行四边形性质可知AD=DF,而AB=3AE,即可知AD=DF=2AE,推出∠ADE=30°,由此可以解题.
(1)证明:∵ 在□ABCD中,AB∥CD,AB=CD,
∵CF=AE,
∴AB-AE=CD-CF,
即 BE=DF,
∵BE∥DF,
∴ 四边形DEBF是□DEBF,
∵DE⊥AB,
∴∠DEB=90,
∴四边形 BFDE 是矩形.
(2)解:∵AF 平分∠BAD,
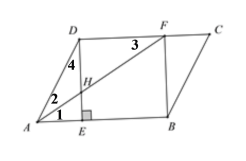
∴∠1=∠2,
∵AB∥CD,
∴∠1=∠3,
∴∠2=∠3,
∴AD=DF,
∵AB=3AE
∴BD=2AE
∵BD=DF,AD=DF
∴AD=2AE,又∠AED=90
∴∠4=30,∠DAE=60
在矩形DEBF中DE=BF=6
∴AE =2![]()
在 RtΔAEH 中,∵∠AEH=90,∠1=![]() ∠DAE=30
∠DAE=30
∴AH=![]() = 4
= 4


科目:初中数学 来源: 题型:
【题目】我们知道平行四边形有很多性质.
现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
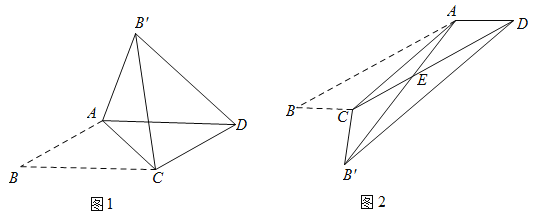
(发现与证明)![]() ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.
ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.
结论1:B′D∥AC;
结论2:△AB′C与![]() ABCD重叠部分的图形是等腰三角形.
ABCD重叠部分的图形是等腰三角形.
……
请利用图1证明结论1或结论2(只需证明一个结论).
(应用与探究)在![]() ABCD中,已知∠B=30°,将△ABC沿AC翻折至△AB′C,连结B′D.
ABCD中,已知∠B=30°,将△ABC沿AC翻折至△AB′C,连结B′D.
(1)如图1,若![]() ,则∠ACB= °,BC= ;
,则∠ACB= °,BC= ;
(2)如图2,![]() ,BC=1,AB′与边CD相交于点E,求△AEC的面积;
,BC=1,AB′与边CD相交于点E,求△AEC的面积;
(3)已知![]() ,当BC长为多少时,是△AB′D直角三角形?
,当BC长为多少时,是△AB′D直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形台球桌面ABCD上有两个球P,Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M,N是球在AB,BC边的撞击点,PQ=4,∠MPQ=30,且点P到AB边的距离为3,则四边形PMNQ的周长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线G:![]() 有最低点。
有最低点。
(1)求二次函数![]() 的最小值(用含m的式子表示);
的最小值(用含m的式子表示);
(2)将抛物线G向右平移m个单位得到抛物线G1。经过探究发现,随着m的变化,抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;
(3)记(2)所求的函数为H,抛物线G与函数H的图像交于点P,结合图像,求点P的纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有![]() 个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
摸球次数( n ) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
摸到白球次( m ) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
白球频率( | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
由上表可以推算出a大约是( )
A.10B.14C.16D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x+2经过点A(m,-2),将点A向右平移7个单位长度,得到点B,抛物线![]() 的顶点为C.
的顶点为C.
(1)求m的值和点B的坐标;
(2)求点C的坐标(用含n的代数式表示);
(3)若抛物线与线段AB只有一个公共点,结合函数图象,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
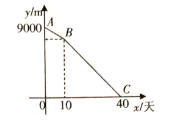
【题目】某街道需要铺设管线的总长为9000![]() ,计划由甲队施工,每天完成150
,计划由甲队施工,每天完成150![]() .工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度
.工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度![]() 与甲队工作时间
与甲队工作时间![]() (天)之间的函数关系图象.
(天)之间的函数关系图象.
(1)直接写出点![]() 的坐标;
的坐标;
(2)求线段![]() 所对应的函数解析式,并写出自变量
所对应的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(3)直接写出乙队工作25天后剩余管线的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有若干个仅颜色不同的红球和黑球,现往一个不透明的袋子里装进2个红球和3个黑球.
(1)随机摸出一个球是黑球的概率为 ;若先从袋子里取出m个红球(不放回),再从袋子里随机摸出一个球,将“摸到黑球”记为事件A.若事件A为必然事件,则m= ;
(2)若先从袋子里摸出一个球,放回后再摸出一个球,用列表法或画树状图法求出两次摸出的球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班50名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计如表所示:
自选项目 | 人数 | 频率 |
立定跳远 | b | 0.18 |
三级蛙跳 | 12 | 0.24 |
一分钟跳绳 | 8 | a |
投掷实心球 | 16 | 0.32 |
推铅球 | 5 | 0.10 |
合计 | 50 | 1 |
(1)求a,b的值;
(2)若该校九年级共有400名学生,试估计年级选择“一分钟跳绳”项目的总人数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至少有一名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com