

分析 (1)首先在BC上截取BG=BE,连接EG,求出∠BGE=45°,即可求出∠CGE=135°;然后根据全等三角形判定的方法,判断出△AEF≌△GCE,求出∠EAF=135°,即可求出∠FAD的度数;
(2)首先延长AF、CD交于点H,判断出∠FAD=45°,进而判断出四边形ABDH是平行四边形,推得DH=AB=CD,即可推得DM是△CFH的中位线,所以FH=2DM;然后在等腰直角三角形HAD中,根据AH=$\sqrt{2}$AD,可推得$\sqrt{2}$AD=AF+2DM.
(3)首先根据AF=8$\sqrt{2}$,AN=10,$\sqrt{2}$AD=AF+2MD,可得$\sqrt{2}$(10+DN)=8$\sqrt{2}$+2MD;然后根据AF∥DM,判断出△AFN∽△DMN,即可判断出$\frac{AN}{DN}=\frac{AF}{DM}$,据此推得DN、MD的关系,求出MD的长为多少即可.
解答 (1)解:在BC上截取BG=BE,连接EG,如图1所示: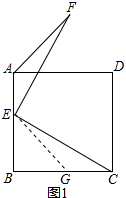 ∵BG=BE,∠EBG=90°,
∵BG=BE,∠EBG=90°,
∴∠BGE=45°,∠CGE=135°,
∵AB=BC,BG=BE,
∴AE=GC,
∵EF⊥EC,
∴∠AEF+∠BEC=90°,
∵∠GCE+∠BEC=90°,
∴∠AEF=∠GCE,
在△AEF和△GCE中,$\left\{\begin{array}{l}{AE=GC}&{\;}\\{∠AEF=∠GCE}&{\;}\\{EF=EC}&{\;}\end{array}\right.$,
∴△AEF≌△GCE(SAS),
∴∠EAF=∠CGE=135°,
∴∠FAD=135°-90°=45°;
(2)证明:延长AF、CD交于点H,如图2所示: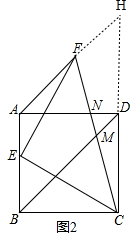 由(1)知,∠EAF=135°,
由(1)知,∠EAF=135°,
∴∠FAD=135°-90°=45°,
∵∠ADB=45°,
∴AH∥BD,
又∵AB∥HD,
∴四边形ABDH是平行四边形,
∴DH=AB=CD,
即D是CH的中点,
∴DM是△CFH的中位线,
∴FH=2DM,
在等腰直角三角形HAD中,
AH=$\sqrt{2}$AD,
∵AH=AF+FH=AF+2DM,
∴$\sqrt{2}$AD=AF+2DM;
(3)解∵AF=8$\sqrt{2}$,AN=10,$\sqrt{2}$AD=AF+2DM,
∴$\sqrt{2}$(10+DN)=8$\sqrt{2}$+2DM,
∵AF∥DM,
∴△AFN∽△DMN,
∴$\frac{AN}{DN}=\frac{AF}{DM}$,即$\frac{10}{DN}=\frac{8\sqrt{2}}{DM}$,
∴DN=$\frac{5\sqrt{2}}{8}$DM,
把DN=$\frac{5\sqrt{2}}{8}$DM代入$\sqrt{2}$(10+DN)=8$\sqrt{2}$+2DM,
整理,解得:DM=$\frac{8\sqrt{2}}{3}$,
∴DN=$\frac{5\sqrt{2}}{8}$×$\frac{8\sqrt{2}}{3}$=$\frac{10}{3}$,
∴AD=AN+DN=10+$\frac{10}{3}$=$\frac{40}{3}$,
∵四边形ABCD是正方形,
∴AB=AD=$\frac{40}{3}$,∠BAD=90°,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{2}$AD=$\frac{40\sqrt{2}}{3}$,
∴BM=BD-DM=$\frac{40\sqrt{2}}{3}$-$\frac{8\sqrt{2}}{3}$=$\frac{32\sqrt{2}}{3}$;
故答案为:$\frac{32\sqrt{2}}{3}$.
点评 本题是四边形综合题,考查了正方形的性质、全等三角形的判定与性质、平行四边形的判定与性质、三角形中位线定理、勾股定理、相似三角形的判定与性质等知识;本题综合性强,有一定难度,证明三角形全等和三角形相似是解决问题的关键.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<1 | B. | a≤1 | C. | a≥1 | D. | a>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
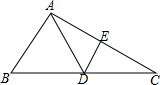 如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )| A. | 13 | B. | 15 | C. | 17 | D. | 19 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com