
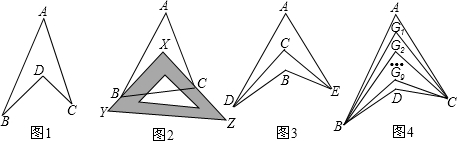
分析 (1)根据题意观察图形连接AD并延长至点F,由外角定理可知,一个三角形的外角等于与它不相邻的两个内角的和,则容易得到∠BDC=∠BDF+∠CDF;
(2)①由(1)的结论可得∠ABX+∠ACX+∠A=∠BXC,然后把∠A=50°,∠BXC=90°代入上式即可得到∠ABX+∠ACX的值.
②结合图形可得∠DBE=∠DAE+∠ADB+∠AEB,代入∠DAE=50°,∠DBE=130°即可得到∠ADB+∠AEB的值,再利用上面得出的结论可知∠DCE=$\frac{1}{2}$(∠ADB+∠AEB)+∠A,易得答案.
③由(2)的方法,进而可得答案.
解答 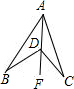 解:(1)连接AD并延长至点F,
解:(1)连接AD并延长至点F,
由外角定理可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD;
且∠BDC=∠BDF+∠CDF及∠BAC=∠BAD+∠CAD;
相加可得∠BDC=∠A+∠B+∠C;
(2)①由(1)的结论易得:∠ABX+∠ACX+∠A=∠BXC,
又因为∠A=50°,∠BXC=90°,
所以∠ABX+∠ACX=90°-50°=40°;
故答案是:40;
②由(1)的结论易得∠DBE=∠A+∠ADB+∠AEB,易得∠ADB+∠AEB=80°;
而∠DCE=$\frac{1}{2}$(∠ADB+∠AEB)+∠A,
代入∠DAE=50°,∠DBE=130°,易得∠DCE=90°;
③∠BG1C═$\frac{1}{10}$(∠ABD+∠ACD)+∠A,
∵∠BG1C=77°,
∴设∠A为x°,
∵∠ABD+∠ACD=140°-x°
∴$\frac{1}{10}$(140-x)+x=77,
14-$\frac{1}{10}$x+x=77,
x=70
∴∠A为70°.
点评 本题考查三角形外角的性质,三角形的内角和定理的应用,能求出∠BDC=∠A+∠B+∠C是解答的关键,注意:三角形的内角和等于180°,三角形的一个外角等于和它不相邻的两个内角的和.


科目:初中数学 来源: 题型:选择题
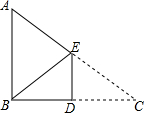 如图,有一张直角三角形纸片ABC,边AB=6,AC=10,∠ABC=90°,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为( )
如图,有一张直角三角形纸片ABC,边AB=6,AC=10,∠ABC=90°,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为( )| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,Rt△ABO中,∠AOB=90°,∠ABO=30°,点A在第二象限,点B在第一象限,过点A的反比例函数表达式为y=-$\frac{1}{x}$,则过点B的反比例函数表达式为y=$\frac{3}{x}$.
如图,Rt△ABO中,∠AOB=90°,∠ABO=30°,点A在第二象限,点B在第一象限,过点A的反比例函数表达式为y=-$\frac{1}{x}$,则过点B的反比例函数表达式为y=$\frac{3}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 全等三角形的对应角相等 | |
| B. | 对顶角相等 | |
| C. | 等边三角形是锐角三角形 | |
| D. | 直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com