解:(1)设BC=x,PC=BC+BP=x+2,PA=4,
∵PA为⊙O的切线,PC为⊙O的割线,
∴PA
2=PB•PC,即16=2(x+2),
解得:x=6,则BC=6;
∵PA为⊙O的切线,
∴∠PAB=∠C,又∠P=∠P,
∴△PBA∽△PAC,
∴

,又PB=2,PA=4,
∴

,
∴AC=2AB,
设AB=k,AC=2k,
∵CB为圆的直径,∴∠CAB=90°,
在Rt△ABC中,由BC=6,
根据勾股定理得:BC
2=AB
2+AC
2,
即36=k
2+4k
2,解得:k=

,
则AB=

;

(2)∵AE为∠CAB的平分线,∴∠CAE=∠BAE,
又∵AP为圆的切线,∴∠PAB=∠C,
∵∠PDA为△CAD的外角,
∴∠PDA=∠C+∠CAE,又∠PAD=∠PAB+∠BAD,
∴∠PAD=∠PDA,
∴PA=PD=4,
∴BD=DP-BP=4-2=2,CD=CB-BD=6-2=4,OD=CD-OC=4-3=1,
连接AO,OE,由PA为圆的切线,得到∠OAP=90°,
∴∠OAE+∠DAP=90°,
∵OA=OE,∴∠OAE=∠OEA,
又∠PAD=∠PDA=∠ODE,
∴∠OEA+∠ODE=90°,
∴∠EOD=90°,
在Rt△EOD中,由OD=1,OE=3,
由勾股定理得DE=

,
由相交弦定理得:AD•DE=BD•CD,
∴AD=

=

=
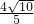
,
则AE=AD+DE=
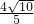
+

=

.
分析:(1)设出BC为x,由BP=2,根据BC+BP表示出PC,再由PA的长,利用切割线定理列出关于x的方程,求出方程的解即可得到BC的长;由PA为圆的切线,根据弦切角等于夹弧所对的圆周角得到一对角相等,再由一对公共角,根据两对对应角相等的两三角形相似可得△PBA∽△PAC,根据相似得比例,把PB和PA的长代入得到AC=2AB,又CB为圆的直径,故所对的圆周角为直角,得到三角形ABC为直角三角形,设AB=k,则AC=2k,再由BC的长,利用勾股定理列出关于k的方程,求出方程的解即可得到k的值,即为AB的长;
(2)由AE为角平分线,根据角平分线的定义得到一对角相等,再由弦切角等于夹弧所对的圆周角得到另一对角相等,根据三角形的外角性质,等量代换及对顶角相等可得∠PAD=∠PDA,根据等角对等边得到PA=PD=4,进而分别求出BD,CD及OD的长,连接OE,OA,由PA为圆的切线,得到∠OAP=90°,即∠OAE+∠DAP=90°,又OE=OA,根据等边对等角得到∠OAE=∠OEA,由刚才得到∠PAD=∠PDA=∠ODE,等量代换可得∠EOD=90°,从而在直角三角形EOD中,由OD与OE的长根据勾股定理求出DE的长,然后利用相交弦定理求出AD的长,由DE+AD即可求出AE的长.
点评:此题综合考查了切线的性质,勾股定理,相似三角形的判定与性质,相交弦定理以及切割线定理,其中见了有切线,圆心切点连,利用切线性质将相切转化为垂直,即构造直角三角形,通过列方程的方法来解决问题中所需的量,此方法称为“构图建模计算法”,要求学生把所学知识融汇贯穿,灵活运用.本题的第三问中注意利用转化的思想来解决角度之间的关系.

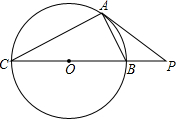 已知:如图,PA为⊙O的切线,A为切点,割线PBC过圆心O,PA=4,PB=2.
已知:如图,PA为⊙O的切线,A为切点,割线PBC过圆心O,PA=4,PB=2. ,又PB=2,PA=4,
,又PB=2,PA=4, ,
, ,
, ;
;
 ,
, =
= =
=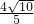 ,
,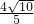 +
+ =
= .
.

 阅读快车系列答案
阅读快车系列答案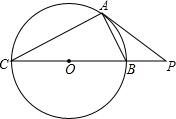 已知:如图,PA为⊙O的切线,A为切点,割线PBC过圆心O,PA=4,PB=2.
已知:如图,PA为⊙O的切线,A为切点,割线PBC过圆心O,PA=4,PB=2. 已知:如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )
已知:如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )



 已知:如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )
已知:如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )







