
阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.

解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线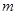 :y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
:y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
(1)y=—2x+6,直线的图象如图:
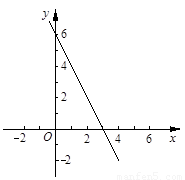
(2)△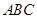 的面积
的面积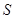 关于的函数表达式为
关于的函数表达式为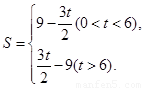
【解析】
试题分析:(1)设直线l的函数表达式为y=k x+b,根据平行的性质可得k=—2,再根据直线l过点(1,4),即可求得直线l的函数表达式,最后根据描点法即可做出直线的图象;
(2)先分别求得直线l分别与y轴、x轴的交点A、B的坐标,再根据l∥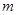 ,可设直线
,可设直线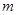 为y=—2x+t,从而表示出C点的坐标为(
为y=—2x+t,从而表示出C点的坐标为(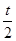 ,0),由t>0可判断C点在x轴的正半轴上,再分C点在B点的左侧与C点在B点的右侧两种情况结合三角形的面积公式分析即可.
,0),由t>0可判断C点在x轴的正半轴上,再分C点在B点的左侧与C点在B点的右侧两种情况结合三角形的面积公式分析即可.
(1)设直线l的函数表达式为y=k x+b.
∵直线l与直线y=—2x—1平行,∴k=—2.
∵直线l过点(1,4),∴—2+b=4,∴b=6.
∴直线l的函数表达式为y=—2x+6,直线的图象如图:
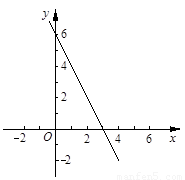
(2)∵直线l分别与y轴、x轴交于点A、B,
∴点A、B的坐标分别为(0,6)、(3,0).
∵l∥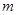 ,∴直线
,∴直线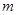 为y=—2x+t.
为y=—2x+t.
∴C点的坐标为(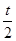 ,0).
,0).
∵t>0,
∴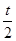 >0.
>0.
∴C点在x轴的正半轴上.
当C点在B点的左侧时,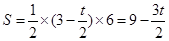 ;
;
当C点在B点的右侧时,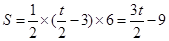 .
.
∴△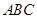 的面积
的面积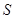 关于的函数表达式为
关于的函数表达式为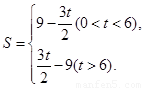
考点:一次函数的综合题
点评:本题知识点多,综合性强,难度较大,主要考查学生对一次函数的知识的熟练掌握情况.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:阅读理解
 我们就称直线l1与直线l2互相平行.解答下面的问题:
我们就称直线l1与直线l2互相平行.解答下面的问题:查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 阅读下面的材料:
阅读下面的材料:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读下面的材料:
阅读下面的材料:查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数![]() 的图象为直线
的图象为直线![]() ,一次函数
,一次函数![]() 的图象为直线
的图象为直线![]() ,若
,若![]() ,且
,且![]() ,我们就称直线
,我们就称直线![]() 与直线
与直线![]() 互相平行.
互相平行.
解答下面的问题:
(1)已知一次函数![]() 的图象为直线
的图象为直线![]() ,求过点
,求过点![]() 且与已知直线
且与已知直线![]() 平行的直线
平行的直线![]() 的函数表达式,并在坐标系中画出直线
的函数表达式,并在坐标系中画出直线![]() 和
和![]() 的图象;
的图象;
(2)设直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,过坐标原点O作OC⊥AB,垂足为C,求
,过坐标原点O作OC⊥AB,垂足为C,求![]() 和
和![]() 两平行线之间的距离OC的长。
两平行线之间的距离OC的长。
(3)若Q为OA上一动点,求QP+QB的最小![]() 值,并求取得最小值时Q点的坐标。
值,并求取得最小值时Q点的坐标。
(4)在![]() 轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案)
轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案)

查看答案和解析>>
科目:初中数学 来源:2011年广东省汕头市潮阳区中考数学模拟试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com