Question

等腰梯形ABCD中，AD∥BC，AB=DC=12，AD=4，∠B=60°，点P是腰AB上的一个动点．
（1）求BC的长．
（2）如图1，如果点M在BC上，BM=12，PM平分梯形ABCD的面积，求出此时PB的长；
（3）过点P作直线PM，是否存在PM将梯形ABCD的周长和面积同时平分？若存在，求出此时PB的长；若不存在，请说明理由；

Answer 1

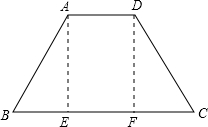
解：（1）过点A作AE⊥BC，DF⊥BC，
∵∠B=60°，AB=12，
∴sin60°=，
∴AE=6，
∴BE=6，同理可证：FC=6，
∴BC=BE+EF+FC=6+4+6=16；

（2）作△PBM的高PG，
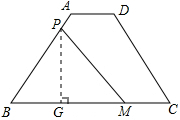
∵等腰梯形ABCD的面积是：（AD+BC）•AE=×（4+16）×6=60
∵PM平分梯形ABCD的面积，
∴S_△PBM=30，
∵BM=12，
∴PG=5，
∵∠B=60°，
∴PB=，
∴PB=10；

（3）当M在BC上时，梯形ABCD的周长是4+12+16+12=44，
∵PB=10，BM=12时PB+BM=22（符合题意），
PB=12，BM=10时 PB+BM=22（符合题意），
当M在DC上时（舍去），
当M在AD上（舍去），
则存在符合题意的直线PM．
分析：（1）先过点A作AE⊥BC，DF⊥BC，根据AB=12，∠B=60°，得出AE的值，同理得出FC的值，即可求出BC的值；
（2）先作△PBM的高PG，根据等腰梯形ABCD的面积的值和PM平分梯形ABCD的面积，求出S_△PBM的值，即可求出PG的值，再根据正弦定理即可求出PB的值；
（3）根据（2）所求出的值，求出梯形ABCD的周长，再根据PB和BM的值来进行判断，正好符合题意，得出结论存在符合题意的直线PM．
点评：此题主要考查学生对等腰梯形的性质及三角形的面积的掌握情况．难度适中，解题关键是掌握三角形的面积公式和等腰梯形的周长．