
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
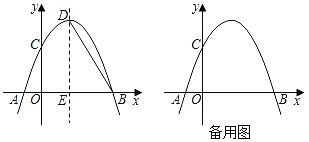
(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=2∠BDE时,求点F的坐标;
(3)若点P是x轴上方抛物线上的动点,以PB为边作正方形PBGH,随着点P的运动,正方形的大小、位置也随着改变,当顶点G或H恰好落在y轴上时,请直接写出点P的横坐标.
【答案】(1)y=﹣![]() x2+x+4;
x2+x+4;![]() ;(2)F(﹣
;(2)F(﹣![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() );(3)P的横坐标为
);(3)P的横坐标为![]() 或2或0或2﹣
或2或0或2﹣![]()
【解析】
(1)将点B、C的坐标代入抛物线表达式,即可求出解析式;将解析式化为顶点式即可得出点D的坐标;
(2)在线段DE上取点M,使MD=MB,此时∠EMB=2∠BDE,则∠FBA=∠EMB,即可求解;
(3)分点P在对称轴右侧、点P在对称轴左侧两种情况,利用三角形全等求解即可.
(1)将点B(4,0)、C(0,4)的坐标代入抛物线表达式得:
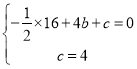 ,解得:
,解得:![]() ,
,
故抛物线的表达式为:y=-![]() x2+x+4=-
x2+x+4=-![]() (x﹣1)2+
(x﹣1)2+![]() ;
;
![]() 点D的坐标为
点D的坐标为![]()
(2)如图1,在线段DE上取点M,使MD=MB,此时∠EMB=2∠BDE,
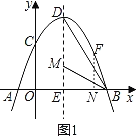
设ME=a,
由(1)得顶点D的坐标为(1,![]() ),
),
∵点B、C的坐标分别为(4,0)、(0,4),
∴BE= BO-EO=4-1=![]() ,
,
∴BM=MD=DE-ME=![]() ,
,
在Rt△BME中,ME2+BE2=BM2,即a2+32=(![]() ﹣a)2,解得:a=
﹣a)2,解得:a=![]() ,
,
∴tan∠EMB= =
=![]() ,
,
过点F作FN⊥x轴于点N,设点F(m,﹣![]() m2+m+4),则FN=|﹣
m2+m+4),则FN=|﹣![]() m2+m+4|,
m2+m+4|,
∵∠FBA=2∠BDE,
∴∠FBA=∠EMB,
∴tan∠FBA=tan∠EMB=![]() ,
,
∵点B(4,0)、点E(1,0),
∴BE=3,BN=4﹣m,
∴tan∠FBA=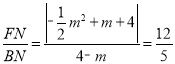 ,
,
解得:m=4(舍去)或﹣![]() 或
或![]() ,
,
故点F(﹣![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() );
);
(3)①当点P在对称轴右侧时,
(Ⅰ)当点H在y轴上时,如图2,
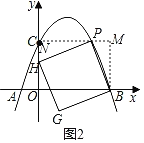
∵∠MPB+∠CPH=90°,∠CPH+∠CHP=90°,
∴∠CHP=∠MPB,
∵∠BMP=∠PNH=90°,PH=BP,
∴△BMP≌△PNH(AAS),
∴MB=PC,
设点P(x,y),则x=y=﹣![]() x2+x+4,
x2+x+4,
解得:x=![]() 或x=
或x=![]() (舍去负值),
(舍去负值),
故点P的横坐标为![]() ;
;
(Ⅱ)当点G在y轴上时,如图3,
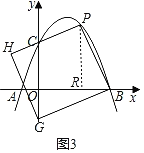
过点P作PR⊥x轴于点R,
同理可得:△PRB≌△BOG(AAS),
∴PR=OB=4,
即yP=4=﹣![]() x2+x+4,
x2+x+4,
解得:x=2;
②当点P在对称轴左侧时,
同理可得:点P的横坐标为0或2﹣![]() ;
;
综上,点P的横坐标为![]() 或2或0或2﹣
或2或0或2﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】随着新冠病毒在全世界蔓延,口罩成为紧缺物资,甲、乙两家工厂积极响应政府号召,准备跨界投资生产口罩.根据市场调查,甲、乙两家工厂计划每天各生产6万片口罩,但由于转型条件不同,其生产的成本不一样,甲工厂计划每生产1万片口罩的成本为0.6万元,乙工厂计划每生产1万片口罩的成本为0.8万元.
(1)按照计划,甲、乙两家工厂共生产2000万片口罩,且甲工厂生产口罩的总成本不高于乙工厂生产口罩的总成本的![]() ,求甲工厂最多可生产多少万片的口罩?
,求甲工厂最多可生产多少万片的口罩?
(2)实际生产时,甲工厂完全按计划执行,但乙工厂的生产情况发生了一些变化.乙工厂实际每天比计划少生产0.5m万片口罩,每生产1万片口罩的成本比计划多0.2m万元,最终乙工厂实际每天生产口罩的成本比计划多1.6万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,二次函数![]() 的图象交x轴于点A,B,交y轴于点C,已知A的横坐标为
的图象交x轴于点A,B,交y轴于点C,已知A的横坐标为![]() .
.
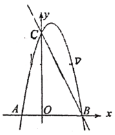
(1)求B点的横坐标和直线![]() 的解析式;
的解析式;
(2)二次函数的图象有一点D,把点D向左平移m(![]() )个单位,将与该二次函数图象上的另一点
)个单位,将与该二次函数图象上的另一点![]() 重合,将
重合,将![]() 向上移动5个单位后,恰好落在直线
向上移动5个单位后,恰好落在直线![]() 上,求m的值.
上,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,小强骑自行车到效外与同学一起游玩.从家出发2小时到达目的地,游玩3小时后按原路以原速返回,小强离家4小时40分钟后,妈妈驾车沿相同路线迎接小强,如图是他们离家的路程y(千米)与时间x(时)的函数图象.已知小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.
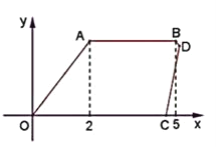
(1)小强家与游玩地的距离是多少?
(2)妈妈出发多长时间与小强相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
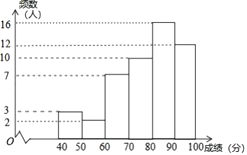
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.
查看答案和解析>>
科目:初中数学 来源: 题型:
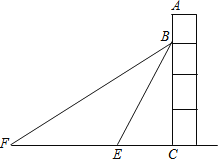
【题目】如图,在某建筑物AC上,竖直挂着“共建文明犍为,共享犍为文明”的宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°,再往条幅方向前行10米到达点E处,看到条幅顶端B,测得仰角为60°,求宣传条幅BC的长(小明的身高不计,结果精确到0.1米).![]() ≈1.732.
≈1.732.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
A. ![]() ≤m<1B.
≤m<1B. ![]() <m≤1C. 1<m≤2D. 1<m<2
<m≤1C. 1<m≤2D. 1<m<2
查看答案和解析>>
科目:初中数学 来源: 题型:
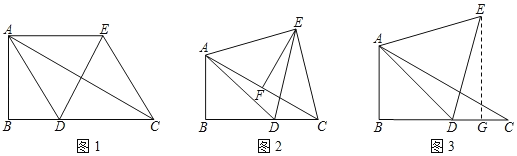
【题目】已知:在Rt△ABC中,∠B=90°,∠ACB=30°,点D为BC边上一动点,以AD为边,在AD的右侧作等边三角形ADE.
(1)当AD平分∠BAC时,如图1,四边形ADCE是 形;
(2)过E作EF⊥AC于F,如图2,求证:F为AC的中点;
(3)若AB=2,
①当D为BC的中点时,过点E作EG⊥BC于G,如图3,求EG的长;
②点D从B点运动到C点,则点E所经过路径长为 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.

(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com