
ЁОЬтФПЁПбДЦкЕНРДЃЌЩНКщБЉЗЂЃЎЯТБэМЧТМСЫФГЫЎПт![]() ФкЫЎЮЛЕФБфЛЏЧщПіЃЌЦфжа
ФкЫЎЮЛЕФБфЛЏЧщПіЃЌЦфжа![]() БэЪОЪБМф(ЕЅЮЛЃК
БэЪОЪБМф(ЕЅЮЛЃК![]() )ЃЌ
)ЃЌ![]() БэЪОЫЎЮЛИпЖШ(ЕЅЮЛЃК
БэЪОЫЎЮЛИпЖШ(ЕЅЮЛЃК![]() )ЃЌЕБ
)ЃЌЕБ![]() ЪБЃЌДяЕНОЏНфЫЎЮЛЃЌПЊЪМПЊеЂЗХЫЎЃЎ
ЪБЃЌДяЕНОЏНфЫЎЮЛЃЌПЊЪМПЊеЂЗХЫЎЃЎ
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 14 | 15 | 16 | 17 | 18 | 14.4 | 12 | 10.3 | 9 | 8 | 7.2 |

(1)дкИјГіЕФЦНУцжБНЧзјБъЯЕжаЃЌИљОнБэИёжаЕФЪ§ОнУшГіЯргІЕФЕуЃЎ
(2)ЧыЗжБ№ЧѓГіПЊеЂЗХЫЎЧАКЭЗХЫЎКѓзюЗћКЯБэжаЪ§ОнЕФКЏЪ§НтЮіЪНЃЎ
(3)ОнЙРМЦЃЌПЊеЂЗХЫЎКѓЃЌЫЎЮЛЕФетжжБфЛЏЙцТЩЛЙЛсГжајвЛЖЮЪБМфЃЌдЄВтКЮЪБЫЎЮЛДяЕН![]() ЃЎ
ЃЎ
ЁОД№АИЁП(1)МћНтЮіЃЛ(2)![]() КЭ
КЭ![]() ЃЛ(3)дЄМЦ
ЃЛ(3)дЄМЦ![]() ЫЎЮЛДяЕН
ЫЎЮЛДяЕН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ИљОнУшЕуЕФЧїЪЦЃЌВТВтКЏЪ§РраЭЃЌЗЂЯжЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гы
гы![]() ПЩФмЪЧвЛДЮКЏЪ§ЙиЯЕЃКЕБ
ПЩФмЪЧвЛДЮКЏЪ§ЙиЯЕЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гы
гы![]() ОЭВЛЪЧвЛДЮКЏЪ§ЙиЯЕЃКЭЈЙ§ЙлВьЪ§ОнЗЂЯж
ОЭВЛЪЧвЛДЮКЏЪ§ЙиЯЕЃКЭЈЙ§ЙлВьЪ§ОнЗЂЯж![]() гы
гы![]() ЕФЙиЯЕзюЗћКЯЗДБШР§КЏЪ§ЃЎ
ЕФЙиЯЕзюЗћКЯЗДБШР§КЏЪ§ЃЎ
(1)дкЦНУцжБНЧзјБъЯЕжаЃЌИљОнБэИёжаЕФЪ§ОнУшГіЯргІЕФЕуЃЌШчЭМЫљЪОЃЎ
(2)ЙлВьЭМЯѓЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гы
гы![]() ПЩФмЪЧвЛДЮКЏЪ§ЙиЯЕЃКЩш
ПЩФмЪЧвЛДЮКЏЪ§ЙиЯЕЃКЩш![]() ЃЌАб
ЃЌАб![]() ЃЌ
ЃЌ![]() ДњШыЕУ
ДњШыЕУ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЕФЙиЯЕЪНЮЊЃК
ЕФЙиЯЕЪНЮЊЃК![]() ЃЌОбщжЄ
ЃЌОбщжЄ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЖМТњзу
ЖМТњзу![]() ЃЌвђДЫЗХЫЎЧА
ЃЌвђДЫЗХЫЎЧА![]() гы
гы![]() ЕФЙиЯЕЪНЮЊЃК
ЕФЙиЯЕЪНЮЊЃК![]() ЃЌЙлВьЭМЯѓЕБ
ЃЌЙлВьЭМЯѓЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гы
гы![]() ОЭВЛЪЧвЛДЮКЏЪ§ЙиЯЕЃКЭЈЙ§ЙлВьЪ§ОнЗЂЯжЃК
ОЭВЛЪЧвЛДЮКЏЪ§ЙиЯЕЃКЭЈЙ§ЙлВьЪ§ОнЗЂЯжЃК![]() .вђДЫЗХЫЎКѓ
.вђДЫЗХЫЎКѓ![]() гы
гы![]() ЕФЙиЯЕзюЗћКЯЗДБШР§КЏЪ§ЃЌЙиЯЕЪНЮЊЃК
ЕФЙиЯЕзюЗћКЯЗДБШР§КЏЪ§ЃЌЙиЯЕЪНЮЊЃК![]() ЃЌЫљвдПЊеЂЗХЫЎЧАКЭЗХЫЎКѓзюЗћКЯБэжаЪ§ОнЕФКЏЪ§НтЮіЪНЮЊЃК
ЃЌЫљвдПЊеЂЗХЫЎЧАКЭЗХЫЎКѓзюЗћКЯБэжаЪ§ОнЕФКЏЪ§НтЮіЪНЮЊЃК![]() КЭ
КЭ![]() .
.
(3)ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌвђДЫдЄМЦ
ЃЌвђДЫдЄМЦ![]() ЫЎЮЛДяЕН
ЫЎЮЛДяЕН![]() ЃЎ
ЃЎ



 ПЊаФПьРжМйЦкзївЕЪюМйзївЕЮїАВГіАцЩчЯЕСаД№АИ
ПЊаФПьРжМйЦкзївЕЪюМйзївЕЮїАВГіАцЩчЯЕСаД№АИ УћЬтбЕСЗЯЕСаД№АИ
УћЬтбЕСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпyЃНЉ![]() x+6ЗжБ№гыxжсЁЂyжсНЛгкЕуAЃЌBЃЎЕБЕуPдкЯпЖЮABЃЈЕуPВЛгыAЃЌBжиКЯЃЉЩЯдЫЖЏЪБЃЌдкзјБъЯЕФкДцдквЛЕуNЃЌЪЙЕУвдOЃЌBЃЌPЃЌNЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЎЧыжБНгаДГіNЕузјБъ_____ЃЎ
x+6ЗжБ№гыxжсЁЂyжсНЛгкЕуAЃЌBЃЎЕБЕуPдкЯпЖЮABЃЈЕуPВЛгыAЃЌBжиКЯЃЉЩЯдЫЖЏЪБЃЌдкзјБъЯЕФкДцдквЛЕуNЃЌЪЙЕУвдOЃЌBЃЌPЃЌNЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЎЧыжБНгаДГіNЕузјБъ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
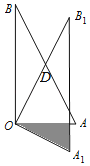
ЁОЬтФПЁПШчЭМЃЌдкЁїOABжаЃЌЁЯAOBЃН90ЁуЃЌAOЃН2ЃЌBOЃН4ЃЎНЋЁїOABШЦЖЅЕуOАДЫГЪБеыЗНЯђа§зЊЕНЁїOA1B1ДІЃЌДЫЪБЯпЖЮOB1гыABЕФНЛЕуDЧЁКУЮЊЯпЖЮABЕФжаЕуЃЌЯпЖЮA1B1гыOAНЛгкЕуEЃЌдђЭМжавѕгАВПЗжЕФУцЛ§__ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
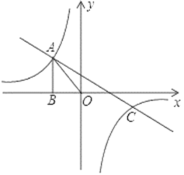
ЁОЬтФПЁПШчЭМЃЌвбжЊЗДБШР§КЏЪ§y1ЃН![]() КЭвЛДЮКЏЪ§y2ЃНk2x+bЕФЭМЯѓЯрНЛгкЕуAЁЂCСНЕуЃЌЦфжаЕуAЕФКсзјБъЮЊЉ2ЃЌЕуCЕФзнзјБъЮЊЉ1ЃЌЙ§ЕуAзїABЁЭxжсгкЕуBЃЌЁїAOBЕФУцЛ§ЮЊ2ЃЎ
КЭвЛДЮКЏЪ§y2ЃНk2x+bЕФЭМЯѓЯрНЛгкЕуAЁЂCСНЕуЃЌЦфжаЕуAЕФКсзјБъЮЊЉ2ЃЌЕуCЕФзнзјБъЮЊЉ1ЃЌЙ§ЕуAзїABЁЭxжсгкЕуBЃЌЁїAOBЕФУцЛ§ЮЊ2ЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЎ
ЃЈ2ЃЉИљОнЭМЯѓжБНгЛиД№ЃКЕБxШЁКЮжЕЪБЃЌвЛДЮКЏЪ§ДѓгкЗДБШР§КЏЪ§ЕФжЕЃЎ
ЃЈ3ЃЉШєAЕуЙигкxжсЕФЖдГЦЕуAЁфдкЖўДЮКЏЪ§y3ЃНЉx2+mx+nЕФЭМЯѓЩЯЃЌЧыХаЖЯЖўДЮКЏЪ§y4ЃНx2+mxЉnЉ3гыxжсЕФНЛЕуИіЪ§ЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГСжвЕВПУХвЊПМВьФГгзУчЕФГЩЛюТЪЃЌгкЪЧНјааСЫЪдбщЃЌЯТБэжаМЧТМСЫетжжгзУчдквЛЖЈЬѕМўЯТвЦжВЕФГЩЛюЧщПіЃЌдђЯТСаЫЕЗЈВЛе§ШЗЕФЪЧЃЈ ЃЉ
вЦжВзмЪ§ | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
ГЩЛюЪ§ | 369 | 1335 | 3203 | 6335 | 8073 | 12628 |
ГЩЛюЕФЦЕТЪ | 0923 | 0.890 | 0915 | 0.905 | 0.897 | 0.902 |
A.гЩДЫЙРМЦетжжгзУчдкДЫЬѕМўЯТГЩЛюЕФИХТЪдМЮЊ0.9
B.ШчЙћдкДЫЬѕМўЯТдйвЦжВетжжгзУч20000жъЃЌдђБиЖЈГЩЛю18000жъ
C.ПЩвдгУЪдбщДЮЪ§РлМЦзюЖрЪБЕФЦЕТЪзїЮЊИХТЪЕФЙРМЦжЕ
D.дкДѓСПжиИДЪдбщжаЃЌЫцзХЪдбщДЮЪ§ЕФдіМгЃЌгзУчГЩЛюЕФЦЕТЪЛсдНРДдНЮШЖЈЃЌвђДЫПЩвдгУЦЕТЪЙРМЦИХТЪ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕФкЃЌЫФБпаЮOABCЪЧОиаЮЃЌЫФБпаЮADEFЪЧе§ЗНаЮЃЌЕуAЃЌDдкxжсЕФе§АыжсЩЯЃЌЕуFдкBAЩЯЃЌЕуBЁЂEОљдкЗДБШР§КЏЪ§yЃН![]() ЃЈkЁй0ЃЉЕФЭМЯѓЩЯЃЌШєЕуBЕФзјБъЮЊ(1ЃЌ6)ЃЌдђе§ЗНаЮADEFЕФБпГЄЮЊЃЈ ЃЉ
ЃЈkЁй0ЃЉЕФЭМЯѓЩЯЃЌШєЕуBЕФзјБъЮЊ(1ЃЌ6)ЃЌдђе§ЗНаЮADEFЕФБпГЄЮЊЃЈ ЃЉ
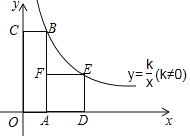
A.1B.2C.4D.6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁбO ЪЧЁїABC ЕФЭтНгдВЃЌO Еудк BC БпЩЯЃЌЁЯBAC ЕФЦНЗжЯпНЛЁбO гкЕу DЃЌСЌНг BDЁЂCDЃЌЙ§Еу D зї BC ЕФЦНааЯпЃЌгы AB ЕФбгГЄЯпЯрНЛгкЕу PЃЎ
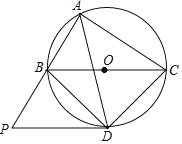
ЃЈ1ЃЉЧѓжЄЃКPD ЪЧЁбO ЕФЧаЯпЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁїPBDЁзЁїDCAЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
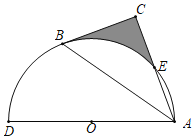
ЁОЬтФПЁПШчЭМЃЌвдADЮЊжБОЖЕФАыдВOОЙ§RtЁїABCаББпABЕФСНИіЖЫЕуЃЌНЛжБНЧБпACгкЕуEЃЛBЁЂEЪЧАыдВЛЁЕФШ§ЕШЗжЕуЃЌ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЯвCDНЛABгкЕуPЃЌAPЃН2ЃЌBPЃН6ЃЌЁЯAPCЃН30ЁуЃЌдђCDЕФГЄЮЊ_______ЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com