
分析 (1)由题意△=(2m+3)2-4m(am+3)=4(1-a)m2+9,所以1-a≥0时,△>0,函数与x轴始终有交点.
(2)当a=-3,b=1时,可得y=mx2-(2m+3)x-3m+1=m(x2-2x-3)-3x+1,由题意x2-2x-3=0,解得x=-1或3,所以无论m为何值,函数始终会经过点(-1,4)和(3,-8).
(3)当a=-1、b=1时,y=mx2-(2m+3)x-m+1,由题意x1+x2=$\frac{2m+3}{m}$,x1x2=$\frac{-m+1}{m}$,推出AB=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(\frac{2m+3}{m})^{2}-4×\frac{-m+1}{m}}$=$\sqrt{9(\frac{1}{m})^{2}+\frac{8}{9}(\frac{1}{m})+8}$=$\sqrt{9(\frac{1}{m}+\frac{4}{9})^{2}+\frac{56}{9}}$,由此即可利用二次函数的性质解决问题.
解答 解:(1)结论:a≤1时,论m为何值.函数与x轴始终有交点,
∵b=3时,函数y=mx2-(2m+3)x+am+3,
又∵△=(2m+3)2-4m(am+3)=4(1-a)m2+9,
∴1-a≥0时,△>0,函数与x轴始终有交点.
(2)当a=-3,b=1时,
y=mx2-(2m+3)x-3m+1
=m(x2-2x-3)-3x+1,
由题意x2-2x-3=0,解得x=-1或3,
∴无论m为何值,函数始终会经过点(-1,4)和(3,-8).
故答案为(-1,4)和(3,-8).
(3)当a=-1、b=1时,y=mx2-(2m+3)x-m+1,
由题意x1+x2=$\frac{2m+3}{m}$,x1x2=$\frac{-m+1}{m}$,
∴AB=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{(\frac{2m+3}{m})^{2}-4×\frac{-m+1}{m}}$
=$\sqrt{9(\frac{1}{m})^{2}+\frac{8}{9}(\frac{1}{m})+8}$
=$\sqrt{9(\frac{1}{m}+\frac{4}{9})^{2}+\frac{56}{9}}$,
∴$\frac{1}{m}$=-$\frac{4}{9}$时,AB的值最小,最小值为$\frac{2\sqrt{14}}{3}$.
∴m=-$\frac{9}{4}$时,AB的值最小.
点评 本题考查二次函数与x轴的交点、二次函数的最值问题等知识,解题的关键是灵活应用所学知识解决问题,学会构建二次函数解决最值问题,所以中考常考题型.


科目:初中数学 来源: 题型:选择题
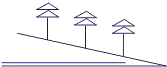 在山坡上植树,要求两棵树间的水平距离是m,测得斜坡的倾斜角为α,则斜坡上相邻两棵树的坡面距离是( )
在山坡上植树,要求两棵树间的水平距离是m,测得斜坡的倾斜角为α,则斜坡上相邻两棵树的坡面距离是( )| A. | $\frac{m}{sinα}$ | B. | $\frac{m}{cosα}$ | C. | m•tanα | D. | m•cosα |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平方根等于本身的数是0 | |
| B. | 如果a,b都是无理数,那么a+b也一定是无理数 | |
| C. | 坐标平面内的点与有序实数对一一对应 | |
| D. | $\sqrt{12}$与6$\sqrt{\frac{1}{27}}$可以合并同类项 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30°,过点G(0,-6)作GF⊥AC,垂足为F,直线GF分别交AB、OC于点E、D,
如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30°,过点G(0,-6)作GF⊥AC,垂足为F,直线GF分别交AB、OC于点E、D,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com