
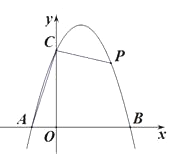
【题目】如图,抛物线 ![]() 与x轴交于点A(-1,0),点B(3,0),与y轴正半轴交于点C.
与x轴交于点A(-1,0),点B(3,0),与y轴正半轴交于点C.
(1)抛物线的解析式为________;
(2)P为抛物线上一点,连结AC,PC,若∠PCO=3∠ACO,点P的坐标为________.
【答案】y=x2+2x+3 (![]() ,
,![]() )
)
【解析】
(1)将A、B两点坐标代入抛物线解析式得一个二元一次方程组,解之即可得出b、c值,从而可得抛物线解析式.
(2)延长CP交x轴于点E,在x轴上取点D,使CD=CA,作EN⊥CD交CD的延长线于点N,作AI⊥CD交CD于I,由等腰三角形三线合一的性质可知
∠DCO=∠ACO,结合已知条件可知∠ACD=∠ECD,由此得tan∠ACD=tan∠ECD,即![]() , 根据等面积法求得AI=
, 根据等面积法求得AI=![]() , 由勾股定理得CI=
, 由勾股定理得CI=![]() , 即
, 即![]() , 由此设EN=3x,则CN=4x,根据tan∠CDO=tan∠EDN得DN=x,由CD=CN-DN求得x值以及E点坐标,再由待定系数法求得直线CE解析式y=-
, 由此设EN=3x,则CN=4x,根据tan∠CDO=tan∠EDN得DN=x,由CD=CN-DN求得x值以及E点坐标,再由待定系数法求得直线CE解析式y=-![]() x+3,将直线CE和抛物线解析式联立、解之即可求得P点坐标.
x+3,将直线CE和抛物线解析式联立、解之即可求得P点坐标.
(1)解:∵A(-1,0),B(3,0)在抛物线上,
∴![]() ,
,
解得:![]()
∴抛物线解析式为:y=x2+2x+3.
故答案为:y=x2+2x+3.(2)延长CP交x轴于点E,在x轴上取点D,使CD=CA,作EN⊥CD交CD的延长线于点N,作AI⊥CD交CD于I,
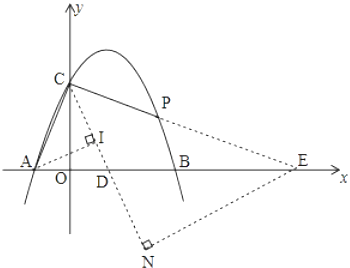
∵CD=CA,OC⊥AD,
∴∠DCO=∠ACO,
∵∠PCO=3∠ACO,
∴∠ACD=∠ECD,
∴tan∠ACD=tan∠ECD,
∴![]() ,
,
在Rt△ACI中,
又∵A(-1,0),C(0,3),
∴OA==OD=1,OC=3,
∴AD=2,AC=DC=![]()
AI=![]() ,
,
∴CI=![]() ,
,
∴![]() ,
,
设EN=3x,则CN=4x,DE=5x,
∵tan∠CDO=tan∠EDN,
∴![]() ,
,
∴DN=x,
∴CD=CN-DN=4x-x=3x=![]() ,
,
∴x=![]() ,
,
即DN=![]() , EN=
, EN=![]() ,
,
∴DE=![]() ,
, ![]()
∴E(![]() , 0),
, 0),
设直线CE解析式为:y=kx+b,
∴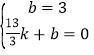 ,
,
解得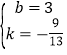 ,
,
∴直线CE解析式为:y=-![]() x+3,
x+3,
∴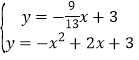 ,
,
解得:![]() (舍去)或
(舍去)或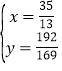 ,
,
∴P(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】(本题满分8分)
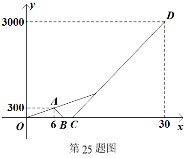
为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题:
⑴小亮在家停留了 分钟.
⑵求小亮骑单车从家出发去图书馆时距家的路程y(米)与出发时间x(分钟)之间的函数关系式.
⑶若小亮和姐姐到图书馆的实际时间为m分钟,原计划步行到达图书馆的时间为n分钟,则n-m= 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计如下,而且制成了如图所示的不完整的统计图.
体育成绩统计表
分数段 | 频数 | 频率 |
A | 12 | 0.05 |
B | 36 | a |
C | 84 | 0.35 |
D | b | 0.25 |
E | 48 | 0.20 |
体育成绩统计图

根据上面提供的信息,解答下列问题:
(1)在统计表中,a=________,b=________,并将统计图补充完整;
(2)小明说:“这组数据的众数一定在C中.”你认为小明的说法正确吗?__________(填“正确”或“错误”).
(3)若成绩在27分以上(含27分)定为优秀,则该市今年48 000名九年级学生中体育成绩为优秀的学生约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块两直角边长分别为AC=3cm和BC=4cm的直角三角形铁皮,要利用它来裁剪一个正方形,有两种方法:一种是正方形的一边在直角三角形的斜边上,另两个顶点在两条直角边上,如图(1);另一种是一组邻边在直角三角形的两直角边上,另一个顶点在斜边上,如图(2).用计算说明两种情形下正方形的面积哪个大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,连接
,连接![]() ,以对角线
,以对角线![]() 为边按逆时针方向作矩形
为边按逆时针方向作矩形![]() ,使矩形
,使矩形![]() 矩形
矩形![]() ;再连接
;再连接![]() ,以对角线
,以对角线![]() 为边,按逆时针方向作矩形,使矩形
为边,按逆时针方向作矩形,使矩形![]() 矩形
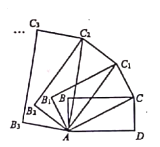
矩形![]() , ..按照此规律作下去,若矩形
, ..按照此规律作下去,若矩形![]() 的面积记作
的面积记作![]() ,矩形
,矩形![]() 的面积记作
的面积记作![]() ,矩形
,矩形![]() 的面积记作
的面积记作![]() , ... 则
, ... 则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
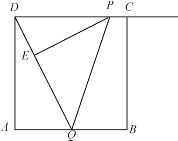
【题目】如图,正方形ABCD,点P为射线DC上的一个动点,点Q为AB的中点,连接PQ,DQ,过点P作PE⊥DQ于点E.
(1)请找出图中一对相似三角形,并证明;
(2)若AB=4,以点P,E,Q为顶点的三角形与△ADQ相似,试求出DP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() (a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里有5个小球,分别标有数字﹣3,﹣2,﹣1,﹣![]() ,﹣
,﹣![]() ,这些小球除所标的数不同外其余都相同,先从盒子随机摸出1个球,记下所标的数,再从剩下的球中随机摸出1个球,记下所标的数.
,这些小球除所标的数不同外其余都相同,先从盒子随机摸出1个球,记下所标的数,再从剩下的球中随机摸出1个球,记下所标的数.
(1)用画树状图或列表的方法求两次摸出的球所标的数之积不大于1的概率.
(2)若以第一次摸出球上的数字为横坐标,第二次摸出球上的数字为纵坐标确定一点,直接写出该点在双曲线y=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
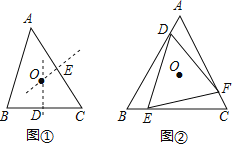
【题目】定义:到一个三角形三个顶点的距离相等的点叫做该三角形的外心.
(1)如图①,小海同学在作△ABC的外心时,只作出两边BC,AC的垂直平分线得到交点O,就认定点O是△ABC的外心,你觉得有道理吗?为什么?
(2)如图②,在等边三角形ABC的三边上,分别取点D,E,F,使AD=BE=CF,连接DE,EF,DF,得到△DEF.若点O为△ABC的外心,求证:点O也是△DEF的外心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com