
如图,在⊙O中,AB是直径,AD是弦,∠ADE = 60°,∠C = 30°.
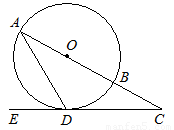
⑴判断直线CD是否是⊙O的切线,并说明理由;
⑵若CD =  ,求BC的长.
,求BC的长.
(1)CD是⊙O的切线.
证明:如图,连接OD.

∵∠ADE=60°,∠C=30°,∴∠A=30°.
∵OA=OD,∴∠ODA=∠A=30°.
∴∠ODE=∠ODA+∠ADE=30°+60°=90°,∴OD⊥CD.
∴CD是⊙O的切线.
(2)解:在Rt△ODC中,∠ODC=90°, ∠C=30°,
CD= .
.
∵tanC=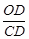 ,
,
∴OD=CD·tanC= ×
× =3.
=3.
∴OC=2OD =6.
∵OB=OD=3,∴BC=OC-OB=6-3=3.
【解析】(1)根据切线的判定定理,连接OD,只需证明OD⊥CD,根据三角形的外角的性质得∠A=30°,再根据等边对等角得∠ADO=∠A,从而证明结论;
(2)在30°的直角三角形OCD中,求得OD,OC的长,则BC=OC-OB.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com