练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB是⊙O的直径，C、D是圆上的两点．若BC=8，cosD= ， 则AB的长为（　　）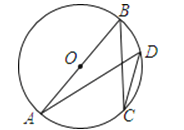

    A.
    B.
    C.
    D.12

    【答案】D
    【解析】解：连接AC，
    由圆周角定理得，∠B=∠D，
    ∵AB是⊙O的直径，
    ∴∠ACB=90°，
    ∴cosB= ， 又BC=8，
    ∴AB=12，
    故选：D．

    【考点精析】关于本题考查的圆周角定理和解直角三角形，需要了解顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：
    在数学课上，老师提出如下问题：
    尺规作图：作Rt△ABC，使其斜边AB=c，一条直角边BC=a．
    已知线段a，c如图．
    小芸的作法如下：
    ①取AB=c，作AB的垂直平分线交AB于点O；
    ②以点O为圆心，OB长为半径画圆；
    ③以点B为圆心，a长为半径画弧，与⊙O交于点C；
    ④连接BC，AC．
    则Rt△ABC即为所求．
    老师说：“小芸的作法正确．”
    请回答：小芸的作法中判断∠ACB是直角的依据是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于实数a、b，定义一种运算“”为：ab=a2 +ab－2，有下列命题：

    ①13=2；

    ②方程x1=0的根为：x1 =－2，x2 =1；

    ③不等式组 的解集为：－1＜x＜4；

    ④点（，）在函数y=x（－1）的图象上．

    其中正确的是（ ）

    A. ①②③④ B. ①③ C. ①②③ D. ③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在购买某场足球赛门票时，设购买门票数为x（张），总费用为y（元）．现有两种购买方案：

    方案一：若单位赞助广告费10000元，则该单位所购门票的价格为每张60元；

    （总费用＝广告赞助费+门票费）

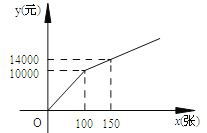
    方案二：购买门票方式如图所示．

    解答下列问题：

    （1）方案一中，y与x的函数关系式为 ；

    方案二中，当0≤x≤100时，y与x的函数关系式为 ，

    当x＞100时，y与x的函数关系式为 ；

    （2）如果购买本场足球赛门票超过100张，你将选择哪一种方案，使总费用最省？请说明理由；

    （3）甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张，花去总费用计58000元，求甲、乙两单位各购买门票多少张．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

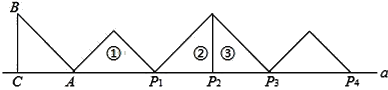
    【题目】如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①可得到点P1，此时AP1=；将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2，此时AP2=+1；将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时，AP3=+2…按此规律继续旋转，直至得到点为止，则=________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l1：y1=﹣x+m与y轴交于点A（0，6），直线l2：y=kx+1分别与x轴交于点B（﹣2，0），与y轴交于点C，两条直线交点记为D．

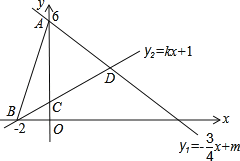
    （1）m=　 　，k=　 　；

    （2）求两直线交点D的坐标；

    （3）根据图象直接写出y1＜y2时自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，定义直线x=m与双曲线yn=的交点Am ， n（m、n为正整数）为“双曲格点”，双曲线yn=在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”．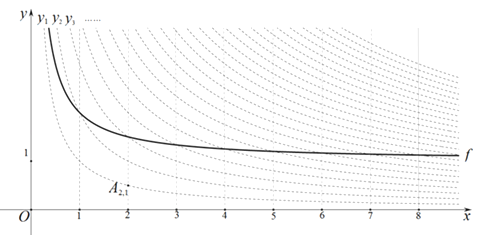

    （1）①“双曲格点”A2 ， 1的坐标为 ；②若线段A4 ， 3A4 ， n的长为1个单位长度，则n= ；
    （2）图中的曲线f是双曲线y1=的一条“派生曲线”，且经过点A2 ， 3 ， 则f的解析式为y=
    （3）画出双曲线y3=的“派生曲线”g（g与双曲线y3=不重合），使其经过“双曲格点”A2 ， a、A3 ， 3、A4 ， b ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，P是线段AB上任一点，AB＝12 cm，C、D两点分别从P、B同时向A点运动，且C点的运动速度为2 cm/s，D点的运动速度为3 cm/s，运动的时间为t s.

    (1)若AP＝8 cm.

    ①运动1 s后，求CD的长；

    ②当D在线段PB运动上时，试说明AC＝2CD；

    (2)如果t＝2 s时，CD＝1 cm，试探索AP的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】列方程或方程组解应用题:

    为了响应学校提出的“节能减排，低碳生活”的倡议，班会课上小李建议每位同学都践行“双面打印，节约用纸”．他举了一个实际例子：打印一份资料，如果用A4厚型纸单面打印，总质量为400克，将其全部改成双面打印，用纸将减少一半；如果用A4薄型纸双面打印，总质量为160克.已知每页薄型纸比厚型纸轻0.8克，求例子中的A4厚型纸每页的质量.（墨的质量忽略不计）

    查看答案和解析>>

    同步练习册答案