
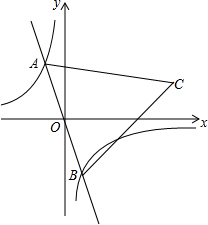
 如图,在反比例函数y=-$\frac{2}{x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动.若tan∠CAB=2,则k的值为( )
如图,在反比例函数y=-$\frac{2}{x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动.若tan∠CAB=2,则k的值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 连接OC,过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,通过角的计算找出∠AOE=∠COF,结合“∠AEO=90°,∠CFO=90°”可得出△AOE∽△COF,根据相似三角形的性质得出$\frac{AE}{CF}=\frac{OE}{OF}=\frac{AO}{CO}$,再由tan∠CAB=$\frac{AO}{CO}$=2,可得出CF•OF=8,由此即可得出结论.
解答 解:连接OC,过点A作AE⊥y轴于点E,过点C作CF⊥x轴于点F,如图所示.
由直线AB与反比例函数y=-$\frac{2}{x}$的对称性可知A、B点关于O点对称,
∴AO=BO.
又∵AC=BC,
∴CO⊥AB.
∵∠AOE+∠EOC=90°,∠EOC+∠COF=90°,
∴∠AOE=∠COF,
又∵∠AEO=90°,∠CFO=90°,
∴△AOE∽△COF,
∴$\frac{AE}{CF}=\frac{OE}{OF}=\frac{AO}{CO}$.
∵tan∠CAB=$\frac{OC}{AO}$=2,
∴CF=2AE,OF=2OE.
又∵AE•OE=|-2|=2,CF•OF=|k|,
∴k=±8.
∵点C在第一象限,
∴k=8.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征、反比例函数的性质以及相似三角形的判定及性质,解题的关键是求出CF•OF=8.本题属于中档题,难度不大,解决该题型题目时,巧妙的利用了相似三角形的性质找出对应边的比例,再结合反比例函数图象上点的坐标特征找出结论.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为2$\sqrt{7}$.
如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为2$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是九(1)班45名同学每周课外阅读时间的频数直方图(每组含前一个边界值,不含后一个边界值).由图可知,人数最多的一组是( )
如图是九(1)班45名同学每周课外阅读时间的频数直方图(每组含前一个边界值,不含后一个边界值).由图可知,人数最多的一组是( )| A. | 2~4小时 | B. | 4~6小时 | C. | 6~8小时 | D. | 8~10小时 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com