
分析 根据等腰三角形的性质和三角形的内角和得到∠BEC=(180°-∠ABC)÷2,∠ADC=(180°-∠DAC)÷2=∠BAC÷2,由外角的性质得到∠DCE=∠BEC-∠ADC,于是得到结论.
解答 解:点D、点E是射线BA上的两个点,如图,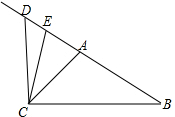
∵BE=BC,∴∠BEC=(180°-∠ABC)÷2,
∵AD=AC,∴∠ADC=(180°-∠DAC)÷2=∠BAC÷2,
∵∠DCE=∠BEC-∠ADC,
∴∠DCE=(180°-∠ABC)÷2-∠BAC÷2=(180°-∠ABC-∠BAC)÷2
=∠ACB÷2=50°÷2=25°,
故答案为:25°.
点评 本题考查了等腰三角形的性质,三角形的内角和,三角形的外角的性质,熟练掌握等腰三角形的性质是解题的关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $a-\frac{1}{3}=b-\frac{1}{3}$ | B. | $-\frac{3}{4}a=-\frac{3}{4}b$ | C. | 3a-1=3b-1 | D. | $\frac{a}{c}=\frac{b}{c}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
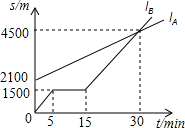 A、B两名同学在一个学校上学,B同学上学的路上经过A同学家.A同学步行,B同学骑自行车,某天,A,B两名同学同时从家出发到学校,如图,lA表示A同学离B同学家的路程sA(m)与行走时间t(min)之间的函数关系图象,lB表示B同学离家的路程sB(m)与行走时间t(min)之间的函数关系图象.
A、B两名同学在一个学校上学,B同学上学的路上经过A同学家.A同学步行,B同学骑自行车,某天,A,B两名同学同时从家出发到学校,如图,lA表示A同学离B同学家的路程sA(m)与行走时间t(min)之间的函数关系图象,lB表示B同学离家的路程sB(m)与行走时间t(min)之间的函数关系图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com