
【题目】用![]() 纸在某誊印社复印文件,复印页数不超过
纸在某誊印社复印文件,复印页数不超过![]() 时每页收费
时每页收费![]() 元;复印页数超过
元;复印页数超过![]() 时,超过部分每页收费
时,超过部分每页收费![]() 元.在某图书馆复印同样的文件,不论复印多少页,每页收费
元.在某图书馆复印同样的文件,不论复印多少页,每页收费![]() 元,如何根据复印的页数选择复印的地点使总价格比较便宜?
元,如何根据复印的页数选择复印的地点使总价格比较便宜?
科目:初中数学 来源: 题型:
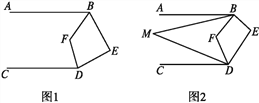
【题目】已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F.
(1)如图1,若∠E=80°,求∠BFD的度数.
(2)如图2,若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
(3)若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
查看答案和解析>>
科目:初中数学 来源: 题型:
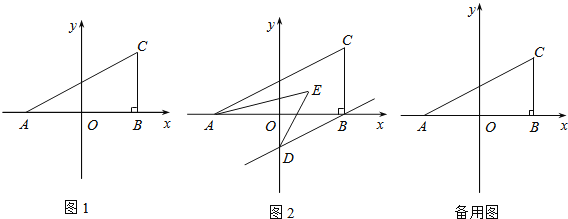
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足![]() ,过C作CB⊥x轴于B,
,过C作CB⊥x轴于B,
(1)求a,b的值;
(2)在y轴上是否存在点P,使得△ABC和△OCP的面积相等,求出P点坐标;
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,
①求:∠CAB+∠ODB的度数;
②求:∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE、BF、DC是直线,B在直线AC上,E在直线DF上,∠1=∠2,∠A=∠F.
求证:∠C=∠D.

证明:因为∠1=∠2(已知),∠1=∠3( )
得∠2=∠3( )
所以AE//_______( )
得∠4=∠F( )
因为__________(已知)
得∠4=∠A
所以______//_______( )
所以∠C=∠D( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x+1)(x﹣m)交x轴于A,B两点(A在B的左侧,m>0),交y轴正半轴于点C,过点C作x轴的平行线交抛物线于另一点E,抛物线的对称轴交CE于点F,以C为圆心画圆,使⊙C经过点(0,2).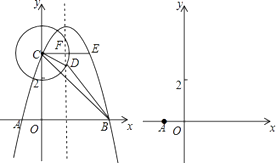
(1)直接写出OB,OC的长.(均用含m的代数式表示)
(2)当m>2时,判断点E与⊙C的位置关系,并说明理由.
(3)当抛物线的对称轴与⊙C相交时,其中下方的交点为D.连结CD,BD,BC.
①当m>3,且C,D,B三点在同一直线上时,求m的值.
②当△BCD是以CD为腰的等腰三角形时,求m的值.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是以O为圆心,AB为直径的半圆的中点,AB=2,等腰直角三角板45°角的顶点与点P重合,当此三角板绕点P旋转时,它的斜边和直角边所在的直线与直径AB分别相交于C,D两点.设线段AD的长为x,线段BC的长为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是两直线y1=2x+6、y2=2x﹣6中某条上的一点,若△APD是等腰Rt△,则点D的坐标为 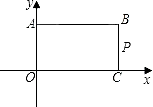
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有 ![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得 ![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: +
,填空: + ![]() =( +
=( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
【答案】(1)![]() ;
;![]() ;(2)4,2,1,1(答案不唯一);(3)
;(2)4,2,1,1(答案不唯一);(3)![]() =7或13
=7或13
【解析】分析:(1)由a+b![]() =(m+n
=(m+n![]() )2,展开比较系数可得答案;
)2,展开比较系数可得答案;
(2)取m=1,n=1,可得a和b的值,可得答案;
(3)由题意得m和n的方程,解方程可得m和n,可得a值.
详解:(1)∵a+b![]() =(m+n
=(m+n![]() )2,
)2,
∴a+b![]() =m2+3n2+2mn
=m2+3n2+2mn![]() ,
,
∴a=m2+3n2,b=2mn.
故答案为:m2+3n2,2mn.
(2)设m=1,n=1,
∴a=m2+3n2=4,b=2mn=2.
故答案为4、2、1、1.
(3)由题意,得:
a=m2+3n2,b=2mn
∵4=2mn,且m、n为正整数,
∴m=2,n=1或者m=1,n=2,
∴a=22+3×12=7,或a=12+3×22=13.
点睛:本题主要考查二次根式的混合运算,完全平方公式,解题的关键在于熟练运算完全平方公式和二次根式的运算法则.
【题型】解答题
【结束】
28
【题目】如图1,已知点A(a,0),B(0,b),且a、b满足![]() ,
,
□ABCD的边AD与y轴交于点E,且E为AD中点,双曲线![]() 经过C、D两点.
经过C、D两点.
(1)若点D点纵坐标为t,则C点纵坐标为 (含t的代数式表示),k的值为 ;
(2)点P在双曲线![]() 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,连接FN,当T在AF上运动时,试判断∠ATH与∠AFN之间的数量关系,并说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
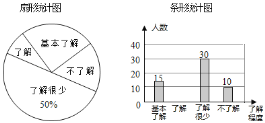
【题目】“校园安全”受到全社会的广泛关注,信丰县某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形圆心角是 度;
(2)请补全条形统计图;
(3)若该中学共有学生1200人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com