
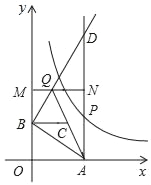
【题目】如图所示,已知:![]() (x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0).动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2
(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0).动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2![]() ,此时P点的坐标为( )
,此时P点的坐标为( )
A. (3,2) B. (![]() ,3
,3![]() ) C. (
) C. (![]() ) D. (
) D. (![]() ,
,![]() )
)
【答案】A
【解析】
首先求出∠BQC=60°,∠BAQ=30°,然后证明△ABQ≌△ANQ,进而求出∠BAO=30°,由S四边形BQNC=2![]() ,求出OA=3,于是求出P点坐标.
,求出OA=3,于是求出P点坐标.
解:连接BN,NC,
四边形BQNC是菱形,
∴BQ=BC=NQ,∠BQC=∠NQC,
∵AB⊥BQ,C是AQ的中点,
∴BC=CQ=12AQ,
∴∠BQC=60°,∠BAQ=30°,
在△ABQ和△ANQ中,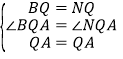 ,
,
∴△ABQ≌△ANQ(SAS),
∴∠BAQ=∠NAQ=30°,
∴∠BAO=30°,
∵S菱形BQNC=2![]() =12×CQ×BN,
=12×CQ×BN,
令CQ=2t=BQ,则BN=2×(2t×![]() )=2
)=2![]() t,
t,
∴t=1
∴BQ=2,
∵在Rt△AQB中,∠BAQ=30°,
∴AB=![]() BQ=2
BQ=2![]() ,
,
∵∠BAO=30°
∴OA=![]() AB=3,
AB=3,
又∵P点在反比例函数y=![]() 的图象上,
的图象上,
∴P点坐标为(3,2).
故选A.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,BD为AC的中线,过点C作
,BD为AC的中线,过点C作![]() 于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.
于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ).

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆八中渝北校区前的同茂大道![]() 的路有一座小山
的路有一座小山![]() ,因工程开发需要爆破.小山
,因工程开发需要爆破.小山![]() 北偏东
北偏东![]() 方向,距小山
方向,距小山![]() 米的
米的![]() 处是同茂大道中央公园东公交站;小山北偏西
处是同茂大道中央公园东公交站;小山北偏西![]() 方向,距小山
方向,距小山![]() 米的
米的![]() 处是同茂大道上麗山公交站.
处是同茂大道上麗山公交站.
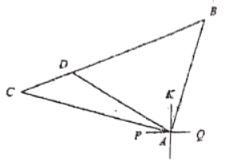
(1)爆破时,在爆破点![]() 周围
周围![]() 米范围有危险请问,为了安全,在爆破小山时需不需要暂时封闭同茂大道
米范围有危险请问,为了安全,在爆破小山时需不需要暂时封闭同茂大道![]() ?请通过计算说明理由;
?请通过计算说明理由;
(2)点![]() 是同茂大道
是同茂大道![]() 上一点(点
上一点(点![]() 不与点
不与点![]() 重合),
重合),![]() ,
,![]() 区域是规划中的公园,问:这个公园占地多少平方米?
区域是规划中的公园,问:这个公园占地多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
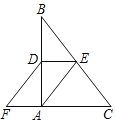
【题目】如图,在Rt△ABC中∠BAC=90°,D,E分别是AB,BC的中点,F在CA的延长线上∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学想法,其中转化思想是中学教学中最活跃,最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法.
问题提出:求边长分别为、![]() 、
、![]() 、
、![]() 的三角形面积.
的三角形面积.
问题解决:
在解答这个问题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为
![]() 、
、![]() 、
、![]() 的格点三角形
的格点三角形![]() (如图),
(如图),![]() 是角边为1和2的直角三角形斜边,
是角边为1和2的直角三角形斜边,![]() 是直角边分别为1和3的直角三角形的斜边,
是直角边分别为1和3的直角三角形的斜边,![]() 是直角边分别为2和3的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求
是直角边分别为2和3的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求![]() 的高,而借用网格就能计算它的面积.
的高,而借用网格就能计算它的面积.
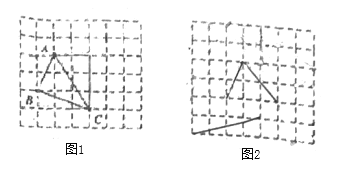
(1)请直接写出图①中![]() 的面积为____________.
的面积为____________.
(2)类比迁移:求边长分别为![]() 、
、![]() 、
、![]() 的三角形面积(请利用图②的正方形网格画出相应的
的三角形面积(请利用图②的正方形网格画出相应的![]() ,并求出它的面积)
,并求出它的面积)
(3)思维拓展:求边长分别为![]() ,的三角形的面积
,的三角形的面积
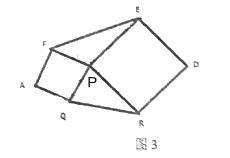
(4)如图(3),已知![]() ,以
,以![]() ,
,![]() 为边向外作正方形
为边向外作正方形![]() ,正方形
,正方形![]() ,连接
,连接![]() ,若
,若![]() ,则六边形
,则六边形 ![]() 的面积是_________.
的面积是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com