
已知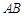 是⊙
是⊙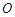 的直径,
的直径,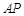 是⊙
是⊙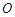 的切线,
的切线,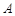 是切点,
是切点, 与⊙
与⊙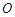 交于点
交于点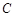 .
.
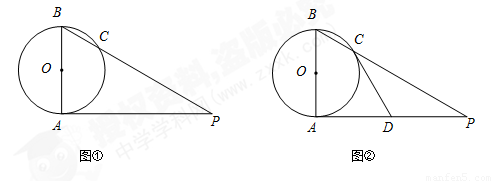
(1)如图①,若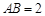 ,
,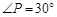 ,求
,求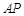 的长(结果保留根号);
的长(结果保留根号);
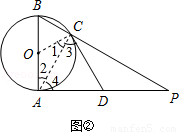
(2)如图②,若 为
为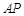 的中点,求证:直线
的中点,求证:直线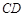 是⊙
是⊙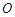 的切线.
的切线.
(1)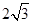 ;(2)证明见试题解析.
;(2)证明见试题解析.
【解析】
试题分析:(1)易证PA⊥AB,再通过解直角三角形求解;
(2)本题连接OC,证出OC⊥CD即可.首先连接AC,得出直角三角形ACP,根据直角三角形斜边上中线等于斜边一半得CD=AD,再利用等腰三角形性质可证∠OCD=∠OAD=90°,从而解决问题.
试题解析:(1)∵AB是⊙O的直径,AP是切线,∴∠BAP=90°.在Rt△PAB中,AB=2,∠P=30°,∴BP=2AB=2×2=4.由勾股定理,得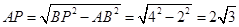 .
.
(2)如图,连接OC、AC.∵AB是⊙O的直径,∴∠BCA=90°,又∵∠ACP=180°﹣∠BCA=90°,在Rt△APC中,D为AP的中点,∴CD=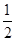 AP=AD,∴∠4=∠3,又∵OC=OA,∴∠1=∠2,∵∠2+∠4=∠PAB=90°,∴∠1+∠3=∠2+∠4=90°,即OC⊥CD.∴直线CD是⊙O的切线.
AP=AD,∴∠4=∠3,又∵OC=OA,∴∠1=∠2,∵∠2+∠4=∠PAB=90°,∴∠1+∠3=∠2+∠4=90°,即OC⊥CD.∴直线CD是⊙O的切线.
考点:1.切线的判定与性质;2.勾股定理.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2012届江苏省丹阳市龙星中学九年级下学期第一次月考数学卷 题型:解答题
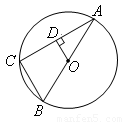
(满分12分)如图,已知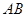 是⊙O的直径,
是⊙O的直径,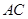 是弦,过点
是弦,过点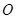 作OD⊥AC于
作OD⊥AC于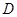 ,连结
,连结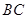 .
.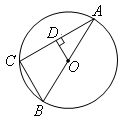
【小题1】(1)求证: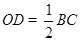 ;
;
【小题2】(2)若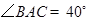 ,求∠
,求∠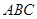 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省丹阳市九年级下学期第一次月考数学卷 题型:解答题
(满分12分)如图,已知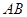 是⊙O的直径,
是⊙O的直径,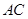 是弦,过点
是弦,过点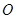 作OD⊥AC于
作OD⊥AC于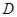 ,连结
,连结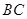 .
.
1.(1)求证: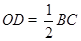 ;
;
2.(2)若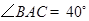 ,求∠
,求∠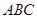 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com