
����Ŀ����֪�����ϵ�A��Ӧ������20����B��Ӧ�����ǩ�30���״�A�������ÿ��1����λ���ȵ��ٶ������˶����Ҵ�B������ÿ��3�����ȵ�λ���ٶ������˶�������������ͬʱ����
��1�����������������˶�3�����
�����������Զʱ�������ڵ�λ�ö�Ӧ������ �������ڵ�λ�ö�Ӧ������
�����Ǿ������ʱ�������ڵ�λ�ö�Ӧ������ �������ڵ�λ�ö�Ӧ������
��2��������ͬʱ���ң�����������������20�����ȵ�λ��
��3�������ҽ�������������ѵ�����״�A�����ܣ�����B�������ת������A�㣬����A���������ת������B���������Ҵ�B�����ܣ�����A�������ת������B�㣬����B���������ת������A������������ͬʱ�������������ܺ����˵ڶ���������ʱ���Ƕ�����

���𰸡���1����23��-39����-21��17����2��15��35����3��37.5s
��������
��1���ٵ����������Զʱ�����ұ������ۣ��������������������У��������Ḻ�������У��ɴ˷ֱ�����������ڵ�λ�ö�Ӧ�������ڵ�����������ʱ�����ϼף�����ͬ����У������Ҷ����������������У��ɴ˷ֱ�����������ڵ�λ�ö�Ӧ������
��2������������������ۣ�
��3���ڶ�������ʱ������·�̺���3��50=150.
���״�A�������ÿ��1����λ���ȵ��ٶ����У��Ҵ�B�������ÿ��3����λ���ȵ��ٶ��˶���������ͬʱ�����˶�3�룬�����˶�·�̣�1��3=3��
���˶�·�̣�3��3=9��
�ٵ����������Զʱ�����ұ������ۣ��������������������У��������Ḻ�������У�
��ʱ�����ڵ�λ�ö�Ӧ����Ϊ20+3=23�������ڵ�λ�ö�Ӧ����Ϊ309=39��
�ڵ�����������ʱ�����ϼף�����ͬ����У������Ҷ����������������У���ʱ�����ڵ�λ�ö�Ӧ����Ϊ20-3=17�������ڵ�λ�ö�Ӧ����Ϊ30+9=-21.
��2����t��������20�����ȵ�λ.
�������֪������δ�ϼף�S��=t��S��=3t��
![]() S��-S��=50-20��
S��-S��=50-20��
��3t-t=30����t=15.
�����ϼײ�������20����λʱ��S��-S��=50+20
��3t-t=70����t=35.
![]() ��t=15��35.
��t=15��35.
��3����x��ʱ���˵ڶ���������
��3+1��x=3��50
x=37.5��s��
�𣺵ڶ�������ʱ��Ҫ37.5s.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ������
�ס�������ͬʱ�����25ǧ��A��ȥB �������ﳵ�Ҳ��������ٶ����ҵ��ٶȵ�3��������B��ͣ��40������Ȼ���B�ط���A������;������������ʱ�����dz�����ʱ��ǡ��3Сʱ�������˵��ٶȸ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���۵�������ֽƬABCD��ʹ��D���ڱ�BC�ϵĵ�F�����ۺ�ΪAE����֪AB=3cm��BC=5cm����EC�ij�Ϊ_____cm��
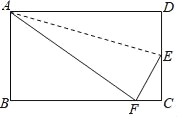
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֻ������̼ƻ�ͬʱ����һ���ס��������ͺ��ֻ���������2�����ͺ��ֻ���5�����ͺ��ֻ��������ʽ�6000Ԫ��������3�����ͺ��ֻ���2�����ͺ��ֻ��������ʽ�4600Ԫ��
��1����ס����ͺ��ֻ�ÿ�����۶���Ԫ��
��2��Ϊ��������õ�ƻ������ס����ͺ��ֻ����ۣ�Ԥ���ò�����1.8��Ԫ�Ҳ�����1.76��Ԫ���ʽ��������ֻ���20���������м��ֽ���������
��3�������ͺ��ֻ����ۼ�Ϊ1500Ԫ�����ͺ��ֻ����ۼ�Ϊ1400Ԫ��Ϊ�˴�������˾����ÿ�۳�һ�����ͺ��ֻ��������˿��ֽ�aԪ�������ͺ��ֻ��ۼ۲��䣬Ҫʹ��2�������з���������ͬ����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ���7����ȫ��ͬ��С������ѳɵ�һ��������A����ͼ��ʾ.
(1) �뻭�����������A������ͼ.
(2) �����˼�����ı������Ϻ���(���������ϵ�һ�治��)�������������Ǻ�ɫ��С��������______��.
(3) �����������ͷ����һЩ��ͬ��С������������ڸü������ϣ�Ҫ���ָ���ͼ������ͼ���䣬������������_______��С������.
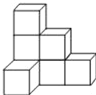
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B��90�㣬AB��7 cm��AC��25 cm.��P�ӵ�A��AB������1 cm/s���ٶ��˶�����B����Q�ӵ�B��BC������6 cm/s���ٶ��˶�����C��P��Q����ͬʱ������
(1)��BC�ij���
(2)����P��Q�˶�2 sʱ����P��Q����֮��ľ��룻
(3)P��Q�����˶�����ʱ��AP��CQ?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������û�е��ܱ�ʾ![]() +1�����������ǿ��������������۴�����С��ʵ������4��ƽ�����ǡ�2����ʽ�ӱ�ʾ��
+1�����������ǿ��������������۴�����С��ʵ������4��ƽ�����ǡ�2����ʽ�ӱ�ʾ��![]() =��2����ij���ľ���ֵ���෴��������ƽ�������������������������0��������ȷ����______��
=��2����ij���ľ���ֵ���෴��������ƽ�������������������������0��������ȷ����______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����O��ֱ��AB��һ������COD��ֱ����OEƽ����BOC��
��1��������ͼ1������AOC=50��������DOE�Ķ�����
������ͼ1������AOC=����ֱ��д����DOE�Ķ������ú����Ĵ���ʽ��ʾ����
��2����ͼ1�е���COD��˳ʱ�뷽����ת��ͼ2��ʾ��λ����
̽����AOC����DOE�Ķ���֮��Ĺ�ϵ��д����Ľ�������˵��������
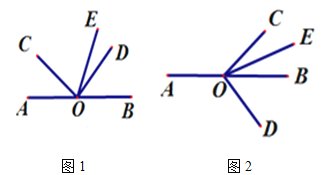
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y= ![]() x2+bx+c��x�ύ��A��5��0����B����1��0�����㣬����A��ֱ��AC��x�ᣬ��ֱ��y=2x�ڵ�C��
x2+bx+c��x�ύ��A��5��0����B����1��0�����㣬����A��ֱ��AC��x�ᣬ��ֱ��y=2x�ڵ�C��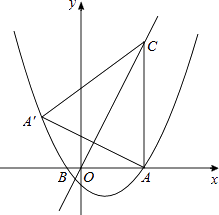
��1����������ߵĽ���ʽ��
��2�����A����ֱ��y=2x�ĶԳƵ�A������꣬�ж���A���Ƿ����������ϣ���˵�����ɣ�
��3����P����������һ���㣬����P��y���ƽ���ߣ����߶�CA���ڵ�M���Ƿ���������ĵ�P��ʹ�ı���PACM��ƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com