
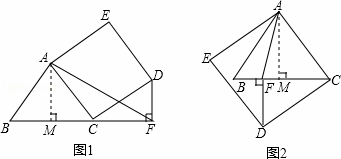
在△ABC中,AB=AC=5,BC=6,以AC为一边作正方形ACDE,过点D作DF⊥BC交直线BC于点F,连接AF,请你画出图形,直接写出AF的长,并画出体现解法的辅助线.
解:如图1所示:
∵AB=AC=5,BC=6,
∴AM=4,
∵∠ACM+∠DCF=90°,∠MAC+∠ACM=90°,
∴∠CAM=∠DCF,
在△AMC和△CFD中
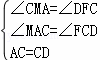 ,
,
∴△AMC≌△CFD(AAS),
∴AM=CF=4,
故AF=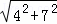 =
=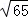 ,
,
如图2所示:
∵AB=AC=5,BC=6,
∴AM=4,MC=3,
∵∠ACM+∠DCF=90°,∠MAC+∠ACM=90°,
∴∠CAM=∠DCF,
在△AMC和△CFD中
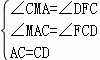 ,
,
∴△AMC≌△CFD(AAS),
∴AM=FC=4,
∴FM=FC﹣MC=1,
故AF=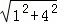 =
=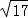 .
.
注:每图1分(图1中没有辅助线、没有直角符号均不给分;图2中没有辅助线、没有直角符号、点B在正方形外均不给分).


科目:初中数学 来源: 题型:
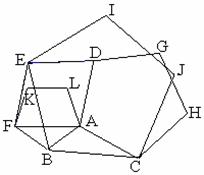
如图,以△ABC的各边为边,在BC的同侧分别作三个正五边形.它们分别是正五边形ABFKL、BCJIE、ACHGD,试探究:
(1)四边形ADEF是什么四边形?
(2)当△ABC满足什么条件时,四边形ADEF是正方形?
(不需证明)
(3)四边形ADEF一定存在吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
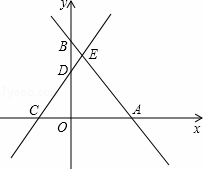
如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2﹣18x+72=0的两根(OA>OC),BE=5,tan∠ABO=.
(1)求点A,C的坐标;
(2)若反比例函数y=的图象经过点E,求k的值;
(3)若点P在坐标轴上,在平面内是否存在一点Q,使以点C,E,P,Q为顶点的四边形是矩形?若存在,请写出满足条件的点Q的个数,并直接写出位于x轴下方的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则所得抛物线的表达式为( )
|
| A. | y=(x+2)2+3 | B. | y=(x﹣2)2+3 | C. | y=(x+2)2﹣3 | D. | y=(x﹣2)2﹣3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
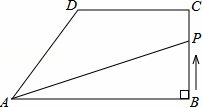
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC﹣CD﹣DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).
(1)当t=2时,求S的值;
(2)当点P在边DA上运动时,求S关于t的函数表达式;
(3)当S=12时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)写出一个只含字母x的代数式,要求此代数式有意义,字母x必须取全体大于1的实数,且此代数式的值恒为正数;
(2)若x是方程x2-x-2=0的根,求(1)中代数式的值.
【设计意图】基础且开放题,考查分式有意义,二次根式的被开方数为非负数,方程的解,考查学生思维的严密性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com