
【题目】如图:直线AB经过点A(0,3)点B( ![]() ,0),点M在y轴上,⊙M经过点A、B,交x轴于另一点C.
,0),点M在y轴上,⊙M经过点A、B,交x轴于另一点C. 
(1)求直线AB的解析式;
(2)求点M的坐标;
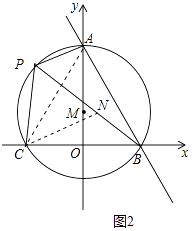
(3)点P是劣弧AC上一个动点,当P点运动时,问:线段PA,PB,PC有什么数量关系?并给出证明.
【答案】
(1)解:设直线AB的解析式为y=kx+b,
把点A(0,3)和点B( ![]() ,0)代入y+kx+b得到
,0)代入y+kx+b得到 ![]() ,
,
解得 ![]() ,
,
∴直线AB的解析式为y=﹣ ![]() x+3
x+3
(2)解:如图1中,连接BM.设AM=BM=r.

在Rt△BMO中,
∵OM2+OB2=BM2,OM=3﹣r,OB= ![]() ,
,
∴(3﹣r)2+( ![]() )2=r2,
)2=r2,
∴r=2,
∴OM=3﹣2=1,
∴点M坐标为(0,1)
(3)解:结论:PB=PA+PC,理由如下:
如图2中,连接AC、在PB上截取PN=PC,连接CN.
∵OM⊥BC,
∴OC=OB,
∴AC=AB,
∵tan∠ABO= ![]() =
= ![]() =
= ![]() ,
,
∴∠ABC=60°,
∴△ABC是等边三角形,
∴AC=CB,∠ACB=∠CAB=60°,
∴∠CPB=∠CAB=60°,∵PC=PN,
∴△PCN是等边三角形,
∴CP=CN,∠PCN=60°,
∴∠PCN=∠ACB=60°,
∴∠PCA=∠NCB,∵PC=CN,CA=CB,
∴△PCA≌△NCB,
∴PA=BN,
∵PB=PN+BN,PN=PC,BN=PA,
∴PB=PA+PC.
【解析】(1)设直线AB的解析式为y=kx+b,把点A(0,3)和点B( ![]() ,0)代入y+kx+b得到
,0)代入y+kx+b得到 ![]() 解方程组即可.(2)如图1中,连接BM.设AM=BM=r.在Rt△BMO中,由OM2+OB2=BM2 , OM=3﹣r,OB=
解方程组即可.(2)如图1中,连接BM.设AM=BM=r.在Rt△BMO中,由OM2+OB2=BM2 , OM=3﹣r,OB= ![]() ,可得(3﹣r)2+(
,可得(3﹣r)2+( ![]() )2=r2 , 解方程即可.(3)结论:PB=PA+PC,如图2中,连接AC、在PB上截取PN=PC,连接CN.首先证明△ACB,△PCN都是等边三角形,再证明△PCA≌△NCB,推出PA=BN,由此即可解决问题.
)2=r2 , 解方程即可.(3)结论:PB=PA+PC,如图2中,连接AC、在PB上截取PN=PC,连接CN.首先证明△ACB,△PCN都是等边三角形,再证明△PCA≌△NCB,推出PA=BN,由此即可解决问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与 CD1交于点O,则线段AD1的长为( ) 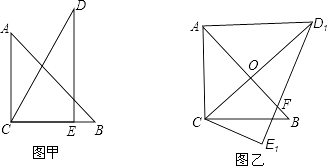
A.6 ![]()
B.10
C.8
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
计算:![]() .
.
解法一:原式=
![]()
解法二:原式=(-![]() )÷[(
)÷[(![]() )-(
)-(![]() )]=
)]=![]() ÷
÷![]() =-
=-![]() ×3=-
×3=-![]() .
.
解法三:原式的倒数为(![]() )÷(-
)÷(-![]() )=
)=![]() ×(-30)-
×(-30)-![]() ×(-30)+
×(-30)+![]() ×(-30)-
×(-30)-![]() ×(-30)=-20+3-5+12=-10,
×(-30)=-20+3-5+12=-10,
故原式=-![]() .
.
(1)上述解法得出的结果不同,肯定有错误的解法,你认为解法________是错误的,在正确的解法中,你认为解法________最简捷;
(2)利用(1)中你认为最简捷的解法计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东方红中学位于东西方向的一条路上,一天我们学校的李老师出校门去家访,他先向西走100米到聪聪家,再向东走150米到青青家,再向西走200米到刚刚家,请问:
(1)如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出聪聪家与青青家的大概位置(数轴上一格表示50米).
(2)聪聪家与刚刚家相距多远?
(3)聪聪家向西20米所表示的数是多少?
(4)你认为可用什么办法求数轴上两点之间的距离?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△AOB,AO=AB=5,OB=6.以O为原点,以OB边所在的直线为x轴,以垂直于OB的直线为y轴建立平面直角坐标系.
(1)求点A的坐标;
(2)若点A关于y轴的对称点为M,点N的横、纵坐标之和等于点A的横坐标,请在图中画出一个满足条件的△AMN,并直接在图上标出点M,N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为准备半期考表彰的奖品,计划从友谊超市购买笔记本和水笔共40件.在获知某网店有“双十一”促销活动后,决定从该网店购买这些奖品.已知笔记本和水笔在这两家商店的零售价分别如下表,且在友谊超市购买这些奖品需花费90元.求从网店购买这些奖品可节省多少元.
品 名 商 店 | 笔记本 (元/件) | 水笔 (元/件) |
友谊超市 | 2.4 | 2 |
网 店 | 2 | 1.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F分别是AB,CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列判断中,错误的是( )

A. ∠AEF=∠EFC B. ∠A=∠BCF C. ∠AEF=∠EBC D. ∠BEF+∠EFC=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了考察甲、乙两种成熟期小麦的株高长势情况,现从中随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲 | 63 | 66 | 63 | 61 | 64 | 61 |
乙 | 63 | 65 | 60 | 63 | 64 | 63 |
(Ⅰ)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(Ⅱ)现将进行两种小麦优良品种杂交实验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对情况,请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com