
分析 (1)、(4)根据正数大于一切负数即可得出结论;
(2)根据负数都小于0即可得出结论;
(3)根据负数与负数比较大小的法则进行比较即可.
解答 解:(1)∵10>0,-1010<0,
∴10>-1 010;
(2)∵-0.25是负数,
∴-0.25<0;
(3)∵|-$\frac{7}{6}$|=$\frac{7}{6}$,|-$\frac{11}{6}$|=$\frac{11}{6}$,$\frac{7}{6}$<$\frac{11}{6}$,
∴-$\frac{7}{6}$>-$\frac{11}{6}$;
(4)∵|-2$\frac{1}{3}$|=2$\frac{1}{3}$>0,-3$\frac{1}{2}$<0,
∴|-2$\frac{1}{3}$|>-3$\frac{1}{2}$.
点评 本题考查的是有理数的大小比较,熟知有理数比较大小的法则是解答此题的关键.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
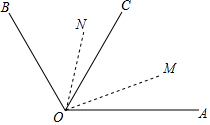 如图,在∠AOB的内部作射线OC,使∠AOC与∠AOB互补,将射线OA,OC同时绕点O分别以每秒12°,每秒8°的速度按逆时针方向旋转,旋转后的射线OA,OC分别记为OM,ON,设旋转时间为t秒.已知t<30,∠AOB=114°.
如图,在∠AOB的内部作射线OC,使∠AOC与∠AOB互补,将射线OA,OC同时绕点O分别以每秒12°,每秒8°的速度按逆时针方向旋转,旋转后的射线OA,OC分别记为OM,ON,设旋转时间为t秒.已知t<30,∠AOB=114°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com