
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在D′处,则重叠部分△AFC的面积是( ) 
A.8
B.10
C.20
D.32
科目:初中数学 来源: 题型:
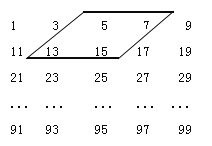
【题目】【题目】如图所示的10![]() 5(行
5(行![]() 列)的数阵,是由一些连续奇数组成的,形如图框中的四个数,设第一行的第一个数为
列)的数阵,是由一些连续奇数组成的,形如图框中的四个数,设第一行的第一个数为![]() .
.
(1)用含![]() 的式子表示另外三个数;
的式子表示另外三个数;
(2)若这样框中的四个数的和是200,求出这四个数;
(3)是否存在这样的四个数,它们的和为246?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积.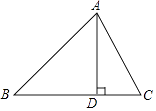
查看答案和解析>>
科目:初中数学 来源: 题型:
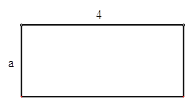
【题目】如图,矩形的长为4,宽为a(a<4),剪去一个边长最大的正方形后剩下一个矩形,同样的方法操作,在剩下的矩形中再剪去一个最大的正方形,若剪去三个正方形后,剩下的恰好是一个正方形,则最后一个正方形的边长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 和双曲线
和双曲线![]() 相交于点A(1,2)和点B(n,-1).
相交于点A(1,2)和点B(n,-1).
(1)求m,k的值;
(2)不等式![]() 的解集为 ;
的解集为 ;
(3)以A、B、O、P为顶点的平行四边形,顶点P的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com