
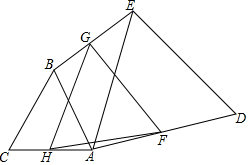
 如图,两个等边△ABC、△ADE(顶点依逆时针方向排列),F、G、H分别是AD、BE、AC的中点,求证:△FGH是等边三角形.
如图,两个等边△ABC、△ADE(顶点依逆时针方向排列),F、G、H分别是AD、BE、AC的中点,求证:△FGH是等边三角形. 分析 如图,连接EC、BD,取EC、BD的中点M、N,想办法证明△FAH≌△GNF,推出FH=FG,△FAH≌△HMG,推出HF=HG,由此即可解决问题.
解答 证明:如图,连接EC、BD,取EC、BD的中点M、N,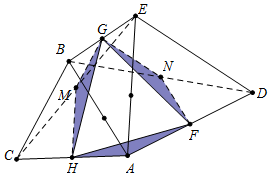
∵△ABC,△ADE都是等边三角形,
∴AB=AC=BC,AD=DE=AE,
∵BG=EG,BN=ND,
∴GN∥DE,GN=$\frac{1}{2}$DE,同理MH=$\frac{1}{2}$AE,
∴GN=HM=AF,同理可证:FN=GM=AH,
∵∠GNF=∠GNB+∠BNF=∠BDE+∠NDF+∠NFD=60°+∠NFD,
∵FN∥AB,
∴∠NFD=∠BAD,
∵∠FAH=∠FAB+∠BAC=60°+∠NFD,
∴∠GNF=FAH,
∴△FAH≌△GNF,
∴FH=FG,
同理可证:△FAH≌△HMG,
∴GH=HF,
∴HF=FG=GH,
∴△HFG是等边三角形.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,利用三角形中位线定理解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
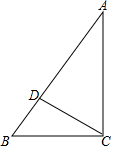 如图,在Rt△ABC中,∠ACB=90°,点D在AB上,将△BCD绕点C按顺时针方向旋转90°后得△ECF.
如图,在Rt△ABC中,∠ACB=90°,点D在AB上,将△BCD绕点C按顺时针方向旋转90°后得△ECF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5{a}^{2}}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{2.5}$ | D. | $\sqrt{{a}^{2}-{b}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| B. | 对角线互相垂直的四边形四边中点顺次连接成的四边形是矩形 | |
| C. | 三个角的度数之比为1:$\sqrt{3}$:2的三角形是直角三角形 | |
| D. | 对角线互相垂直的平行四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 35x+70y=1225 | B. | 70x+35y=1225 | C. | 70x-35y=1225 | D. | 35x-70y=1225 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 采用全面调查方式 | |
| B. | 个体是每名学生 | |
| C. | 样本容量是350 | |
| D. | 估计该校七年级学生中约有35名学生的作业不合格 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com