
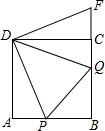
 ��ͼ���ڱ߳�Ϊ8cm��������ABCD�У�����P�ӵ�A���������߶�AB��ÿ��1cm���ٶ����B�˶���ͬʱ����Q�ӵ�B���������߶�BC��ÿ��3cm���ٶ����C�˶�������Q����C��ʱ����Pͬʱֹͣ�����˶�ʱ��Ϊt�룮
��ͼ���ڱ߳�Ϊ8cm��������ABCD�У�����P�ӵ�A���������߶�AB��ÿ��1cm���ٶ����B�˶���ͬʱ����Q�ӵ�B���������߶�BC��ÿ��3cm���ٶ����C�˶�������Q����C��ʱ����Pͬʱֹͣ�����˶�ʱ��Ϊt�룮���� ��1����֪BQ=3t����CQ=BC-BQ�ɱ�ʾ��CQ��
��2������t�ɷֱ��ʾ��AP��CQ���Ӷ��ɱ�ʾ����ADP�͡�DFQ��������ɵõ�����t�ķ��̣������t��ֵ������������֪��DAP�ա�DCQ����AP=CQ�����t��ֵ����Rt��BPQ�У������PQ�ij�����һ�����жϡ�PDQ���FDQ��ȫ�ȣ�
��� �⣺
��1�����ı���ABCDΪ�����Σ�
��AB=BC=AD=CD=8cm��
���˶�t��ʱ����BQ=3tcm��
��CQ=BC-BQ=��8-3t��cm��
�ʴ�Ϊ����8-3t����
��2�����������֪CQ=CF��
��QF=2CQ=2��8-3t��cm����AP=tcm��
��S��ADP=$\frac{1}{2}$AD•AP=4t��S��DFQ=$\frac{1}{2}$QF•CD=8��8-3t����
��S��ADP=S��DFQ��
��4t=8��8-3t����
���t=$\frac{16}{7}$��
�ڵ�DP��DFʱ�����С�ADP+��PDQ=��PDQ+��CDF��
���ADP=��CDF���ҡ�DAP=��DCF=90�㣬
�ڡ�DAP�͡�DCF��
$\left\{\begin{array}{l}{��ADP=��CDF}\\{AD=CD}\\{��DAP=��DCF}\end{array}\right.$
���DAP�ա�DCF��ASA����
��CF=AP=CQ��
��t=8-3t�����t=2�룬
��BP=BQ=6cm��QF=2CQ=4cm��
��Rt��BPQ�У��ɹ��ɶ��������PQ=6$\sqrt{2}$��
�ڡ�PDQ�͡�FDQ�У�PD=DF��DQ=DQ����PQ��QF��
���PDQ���FDQ��ȫ�ȣ���PDQ��45�㣮
���� ����Ϊ�ı��ε��ۺ�Ӧ�ã��漰֪ʶ���������ε����ʡ�ȫ�������ε��ж������ʡ����ɶ����ȣ������˶��͵����⣬��ʱ��t��ʾ����Ӧ���߶εij��ȣ�����Ϊ���ǽ���Ĺؼ������⿼��֪ʶ���Ϊ�������ѶȲ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
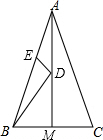 ��ͼ����ABC�У�AB=AC=4����BAC=45�㣬AMƽ�֡�BAC����D��E �ֱ�ΪAM��AB�ϵĶ��㣬��BD+DE����Сֵ��2$\sqrt{2}$��
��ͼ����ABC�У�AB=AC=4����BAC=45�㣬AMƽ�֡�BAC����D��E �ֱ�ΪAM��AB�ϵĶ��㣬��BD+DE����Сֵ��2$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD�У���P�ǶԽ���BD��һ�㣬PE��AB�ڵ�E��PE=3�����P��BC�ľ������3��
��ͼ��������ABCD�У���P�ǶԽ���BD��һ�㣬PE��AB�ڵ�E��PE=3�����P��BC�ľ������3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{\frac{x}{60}+\frac{y}{80}=15}\\{\frac{y}{40}+\frac{x}{60}=10}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{\frac{x}{60}+\frac{y}{80}=10}\\{\frac{y}{80}+\frac{x}{40}=15}\end{array}\right.$ | ||
| C�� | $\left\{\begin{array}{l}{\frac{x}{60}+\frac{y}{80}=10}\\{\frac{y}{40}+\frac{x}{60}=15}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{\frac{x}{40}+\frac{y}{80}=10}\\{\frac{y}{40}+\frac{x}{60}=15}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com