
【题目】东坡商贸公司购进某种水果成本为20元/![]() ,经过市场调研发现,这种水果在未来48天的销售单价
,经过市场调研发现,这种水果在未来48天的销售单价![]() (元/
(元/![]() )与时间
)与时间![]() (天)之间的函数关系式
(天)之间的函数关系式 ,
,![]() 为整数,且其日销售量
为整数,且其日销售量![]() (
(![]() )与时间
)与时间![]() (天)的关系如下表:
(天)的关系如下表:
时间 | 1 | 3 | 6 | 10 | 20 | … |
日销售量 | 118 | 114 | 108 | 100 | 80 | … |
(1)已知![]() 与
与![]() 之间的变化符合一次函数关系,试求在第30天的日销售量;
之间的变化符合一次函数关系,试求在第30天的日销售量;
(2)哪一天的销售利润最大?最大日销售利润为多少?
【答案】(1)第30天的日销售量为![]() ;(2)当
;(2)当![]() 时,
时,![]()
【解析】
(1)设y=kt+b,利用待定系数法即可解决问题.
(2)日利润=日销售量×每kg利润,据此分别表示前24天和后24天的日利润,根据函数性质求最大值后比较得结论.
(1)设y=kt+b,把t=1,y=118;t=3,y=114代入得到:
![]()
解得,![]() ,
,
∴y=-2t+120.
将t=30代入上式,得:y=-2×30+120=60.
所以在第30天的日销售量是60kg.
(2)设第![]() 天的销售利润为
天的销售利润为![]() 元,则
元,则![]()
当![]() 时,由题意得,
时,由题意得,![]()
=![]()
=![]()
∴t=20时,w最大值为1600元.
当![]() 时,
时,![]()
∵对称轴t=44,a=2>0,
∴在对称轴左侧w随t增大而减小,
∴t=25时,w最大值为210元,
综上所述第20天利润最大,最大利润为1600元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
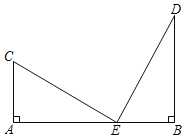
【题目】如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=3,AC=2,AB=m,在线段AB上找一点E,使△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具商店以每件60元为成本购进一批新型玩具,以每件100元的价格销售则每天可卖出20件,为了扩大销售,增加盈利,尽快减少库存,商店决定采取适当的降价措施,经调查发现:若每件玩具每降价1元,则每天可多卖2件.
(1)若商店打算每天盈利1200元,每件玩具的售价应定为多少元?
(2)若商店为追求效益最大化,每件玩具的售价定为多少元时,商店每天盈利最多?最多盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学课外活动小组的同学.利用所学的数学知识,测底部可以到达的学校操场上的旗杆AB高度,他们采用了如下两种方法:
方法1:在地面上选一点C,测得CB为40米,用高为1.6米的测角仪在C处测得旗杆顶部A的仰角为28°;
方法2:在相同时刻测得旗杆AB的影长为17.15米,又测得已有的2米高的竹杆的影长为1.5米.
你认为这两种方法可行吗?若可行,请你任选一种方法算出旗杆高度(精确到0.1米)若不可行,自己另设计一种测量方法(旗杆顶端不能到达),算出旗杆高度(结果可用字母表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
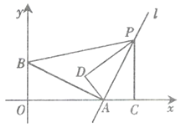
【题目】如图,在直角坐标系中,点![]() ,点
,点![]() ,过点
,过点![]() 的直线
的直线![]() 垂直于线段
垂直于线段![]() ,点
,点![]() 是直线
是直线![]() 上在第一象限内的一动点,过点
上在第一象限内的一动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,把
,把![]() 沿
沿![]() 翻折
翻折![]() ,使点
,使点![]() 落在点
落在点![]() 处,若以
处,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与△ABP相似,则满足此条件的点
为顶点的三角形与△ABP相似,则满足此条件的点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是直径,OD⊥AC,垂足为D点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PB,PC,且满足∠PCA=∠ABC
(1)求证:PA=PC;
(2)求证:PA是⊙O的切线;
(3)若BC=8,![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机微信推出了红包游戏,它有多种玩法,其中一种为“拼手气红包”,用户设好总金额以及红包个数后,可以生成不等金额的红包,现有一用户发了三个“拼手气红包”,总金额为3元,随机被甲、乙、丙三人抢到.
(1)下列事件中,确定事件是 ,①丙抢到金额为1元的红包;②乙抢到金额为4元的红包;③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多
(2)记金额最多、居中、最少的红包分别为A,B,C.求甲抢到红包A,乙抢到红包C的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两名同学在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制出统计图如图所示,则符合这一结果的试验可能是( )
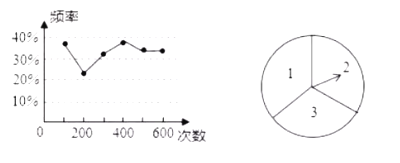
A.抛一枚硬币,正面朝上的概率
B.掷一枚正六面体的骰子,出现![]() 点的概率
点的概率
C.转动如图所示的转盘,转到数字为奇数的概率
D.从装有![]() 个红球和
个红球和![]() 个蓝球的口袋中任取一个球恰好是蓝球的概率
个蓝球的口袋中任取一个球恰好是蓝球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
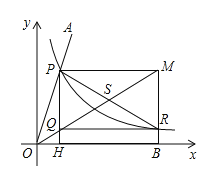
【题目】“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数![]() 的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=![]() ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题:
(1)设P(![]() ,
,![]() )、R(
)、R(![]() ,
,![]() ),求直线OM对应的函数表达式(用含
),求直线OM对应的函数表达式(用含![]() ,
,![]() 的代数式表示);
的代数式表示);
(2)分别过点P和R作y轴和x轴的平行线,两直线相交于点Q.请说明Q点在直线OM上,并据此证明∠MOB=![]() ∠AOB;
∠AOB;
(3)应用上述方法得到的结论,你如何三等分一个钝角(用文字简要说明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com