
【题目】(已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
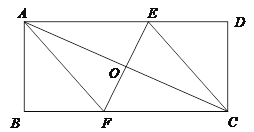
(1)求证:四边形AFCE是菱形;
(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;
(3)在线段AC上是否存在一点P,使得2AE2=AC·AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
【答案】(1)证明见解析;(2)24cm;(3)存在,过E作EP⊥AD交AC于P,则P就是所求的点,证明见解析.
【解析】
(1)由四边形ABCD是矩形与折叠的性质,易证得△AOE≌△COF,即可得AE=CF,则可证得四边形AFCE是平行四边形,又由AC⊥EF,则可证得四边形AFCE是菱形;
(2)由已知可得:S△ABF=![]() ABBF=24cm2,则可得AB2+BF2=(AB+BF)2-2ABBF=(AB+BF)2-2×48=AF2=100(cm2),则可求得AB+BF的值,继而求得△ABF的周长.
ABBF=24cm2,则可得AB2+BF2=(AB+BF)2-2ABBF=(AB+BF)2-2×48=AF2=100(cm2),则可求得AB+BF的值,继而求得△ABF的周长.
(3)过E作EP⊥AD交AC于P,则P就是所求的点,首先证明四边形AFCE是菱形,然后根据题干条件证明△AOE∽△AEP,列出关系式.
解:(1)∵四边形ABCD是矩形,
∴AD∥BC,∴∠EAO=∠FCO,
由折叠的性质可得:OA=OC,AC⊥EF,
在△AOE和△COF中,
∵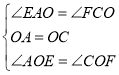 ,
,
∴△AOE≌△COF(ASA),
∴AE=CF,
∴四边形AFCE是平行四边形,
∵AC⊥EF,
∴四边形AFCE是菱形;
(2)∵四边形AFCE是菱形,
∴AF=AE=10cm,
∵四边形ABCD是矩形,
∴∠B=90°,
∴S△ABF=![]() ABBF=24cm2,
ABBF=24cm2,
∴ABBF=48(cm2),
∴AB2+BF2=(AB+BF)2-2ABBF=(AB+BF)2-2×48=AF2=100(cm2),
∴AB+BF=14(cm)
∴△ABF的周长为:AB+BF+AF=14+10=24(cm).
(3)证明:过E作EP⊥AD交AC于P,则P就是所求的点.
当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°,
∵在平行四边形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
∴△AOE≌△COF,
∴OE=OF
∴四边形AFCE是菱形.
∴∠AOE=90°,又∠EAO=∠EAP,
由作法得∠AEP=90°,
∴△AOE∽△AEP,
∴![]() ,则AE2=AOAP,
,则AE2=AOAP,
∵四边形AFCE是菱形,
∴AO=![]() AC,
AC,
∴AE2=![]() ACAP,
ACAP,
∴2AE2=ACAP.


科目:初中数学 来源: 题型:
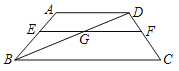
【题目】如图,在梯形ABCD中,点E,F分别在边AB,CD上,AD∥EF∥BC,EF与BD交于点G,AD=5,BC=10,![]() =
=![]() .
.
(1)求EF的长;
(2)设![]() =
=![]() ,
,![]() =
=![]() ,那么
,那么![]() = ,
= ,![]() = .(用向量
= .(用向量![]() 、
、![]() 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:将函数l的图象绕点P(m,0)旋转180°,得到新的函数l'的图象,我们称函数l'是函数关于点P的相关函数.
例如:当m=1时,函数y=(x+1)2+5关于点P(1,0)的相关函数为y=﹣(x﹣3)2﹣5.
(1)当m=0时
①一次函数y=x﹣1关于点P的相关函数为 ;
②点(![]() ,﹣
,﹣![]() )在二次函数y=﹣ax2﹣ax+1(a≠0)关于点P的相关函数的图象上,求a的值.
)在二次函数y=﹣ax2﹣ax+1(a≠0)关于点P的相关函数的图象上,求a的值.
(2)函数y=(x﹣1)2+2关于点P的相关函数y=﹣(x+3)2﹣2,则m= ;
(3)当m﹣1≤x≤m+2时,函数y=x2﹣mx﹣![]() m2关于点P(m,0)的相关函数的最大值为6,求m的值.
m2关于点P(m,0)的相关函数的最大值为6,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
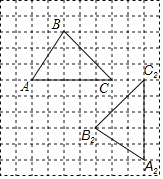
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC为格点三角形(顶点在网格线的交点).
(1)将△ABC向上平移2个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕着某点O逆时针方向旋转90°后,得到△A2B2C2,请画出旋转中心O,并直接写出在此旋转过程中,线段AB扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…,按照此规律,第n个图中正方形和等边三角形的个数之和为( )个.

A.9nB.6nC.9n+3D.6n+3
查看答案和解析>>
科目:初中数学 来源: 题型:
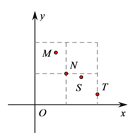
【题目】“单词的记忆效率”是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.右图描述了某次单词复习中![]() 四位同学的单词记忆效率
四位同学的单词记忆效率![]() 与复习的单词个数
与复习的单词个数![]() 的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MAN=30°,在射线AN上取一点B,使AB=4 cm,过点B作BC⊥AM于点C,点D为边AB上的动点(点D不与点A,点B重合),连接CD,过点D作ED⊥CD交直线AC于点E.在点D由点A到点B运动过程中,设AD=x cm,AE=y cm.
(1)取指定点作图,根据下面表格预填结果,先通过作图确定AD=2 cm时,点E的位置,测量AE的长度.
①根据题意,在答题卡上补全图形;
②把表格补充完整:通过取点、画图、测量,得到了x与y的几组对应值,如表:
x/cm | … |
| 1 |
| 2 |
| 3 |
| … |
y cm | … | 0.4 | 0.8 | 1.0 | m | 1.0 | 0 | 4.0 | … |
则m=______(结果保留一位小数).
(2)在下面的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为______cm.
AD时,AD的长度约为______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
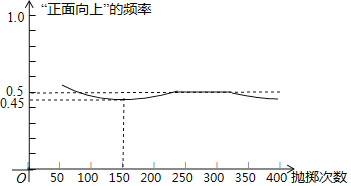
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A.①B.②C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从共享单车,共享汽车等共享出行到共享充电宝,共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速普及应用,越来越多的企业与个人成为参与者与受益者.小宇和小强分别对共享经济中的“共享出行”和“共享知识”最感兴趣,他们上网查阅了相关资料,顺便收集到四个共享经济领域的图标,并将其制成编号为![]() ,
,![]() ,
,![]() ,
,![]() 的四张卡片(除编号和内容外,其余完全相同)他们将这四张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率(这四张卡片分别用它们的编号
的四张卡片(除编号和内容外,其余完全相同)他们将这四张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率(这四张卡片分别用它们的编号![]() ,
,![]() ,
,![]() ,
,![]() 表示)
表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com