
【题目】如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
(1)求证:△PCE≌△EDQ;
(2)延长PC,QD交于点R.如图2,若∠MON=150°,求证:△ABR为等边三角形;
(3)如图3,若△ARB∽△PEQ,求∠MON大小
【答案】
(1)证明:∵点C、D、E分别是OA,OB,AB的中点,
∴DE=OC,∥OC,CE=OD,CE∥OD,
∴四边形ODEC是平行四边形,
∴∠OCE=∠ODE,
∵△OAP,△OBQ是等腰直角三角形,
∴∠PCO=∠QDO=90°,
∴∠PCE=∠PCO+∠OCE=∠QDO=∠ODQ=∠EDQ,
∵PC= ![]() AO=OC=ED,CE=OD=
AO=OC=ED,CE=OD= ![]() OB=DQ,
OB=DQ,
在△PCE与△EDQ中,
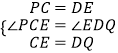 ,
,
∴△PCE≌△EDQ;
(2)解:如图2,连接RO,
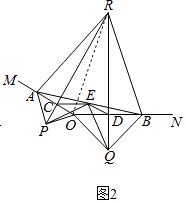
∵PR与QR分别是OA,OB的垂直平分线,
∴AP=OR=RB,
∴∠ARC=∠ORC,∠ORQ=∠BRO,
∵∠RCO=∠RDO=90°,∠COD=150°,
∴∠CRD=30°,
∴∠ARB=60°,
∴△ARB是等边三角形;
(3)解:如图3中,

由(1)得,EQ=EP,∠DEQ=∠CPE,
∴∠PEQ=∠CED﹣∠CEP﹣∠DEQ=∠ACE﹣∠CEP﹣∠CPE=∠ACE﹣∠RCE=∠ACR=90°,
∴△PEQ是等腰直角三角形,
∵△ARB∽△PEQ,
∴∠ARB=∠PEQ=90°,
∴∠OCR=∠ODR=90°,∠CRD= ![]() ∠ARB=45°,
∠ARB=45°,
∴∠MON=180°﹣∠CRD=135°.
【解析】(1)此小题关键是根据三角形的中位线的性质得到得出四边形ODEC是平行四边形,于是得到∠OCE=∠ODE,根据等腰直角三角形得到∠PCO=∠QDO=90°,PC=ED,CE=DQ,即可得到结论;
(2)连接RO,由垂直平分线的性质,得到AP=OR=RB,再由等腰三角形的性质得到∠ARC=∠ORC,∠ORQ=∠BRO,在四边形CRDO中得到∠CRD=30°,即可得到结论;
(3)由(1)得EQ=EP,∠DEQ=∠CPE,推出∠PEQ=∠ACR=90°,证得△PEQ是等腰直角三角形,根据相似三角形的性质得到∠ARB=∠PEQ=90°,从而求得∠MON的度数.
【考点精析】通过灵活运用平行四边形的判定与性质和相似三角形的判定与性质,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪.如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.平面直角坐标系![]() 为原点,长方形
为原点,长方形![]() 的顶点
的顶点![]() 在坐标轴上,点
在坐标轴上,点![]() ,
,![]() ,且己知
,且己知![]() 是64的立方根,
是64的立方根,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)如图1,有两动点![]() 点从
点从![]() 点出发沿
点出发沿![]() 轴负方向以1个单位长度每秒的速度匀速移动,
轴负方向以1个单位长度每秒的速度匀速移动,![]() 点从
点从![]() 点出发以2个单位长度每秒的速度沿
点出发以2个单位长度每秒的速度沿![]() 的路线匀速移动,
的路线匀速移动,![]() 点到达
点到达![]() 点整个运动随之结束.若长方形对角线
点整个运动随之结束.若长方形对角线![]() 的交点
的交点![]() 的坐标是
的坐标是![]() ,设运动时间为
,设运动时间为![]() 秒,问:以
秒,问:以![]() 为顶点的多边形面积是否为定值,若是,请求出此多边形的面积;若不是,请说明理由.
为顶点的多边形面积是否为定值,若是,请求出此多边形的面积;若不是,请说明理由.
(3)如图2,![]() 是线段
是线段![]() 上一点,使
上一点,使![]() ,点
,点![]() 是线段
是线段![]() 上任意一点(
上任意一点(![]() 不与点
不与点![]() 重合),连接
重合),连接![]() 交
交![]() 于点
于点![]() .已知
.已知![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若坡角∠FAE=30°,求大树的高度(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ![]() ≈1.73)
≈1.73)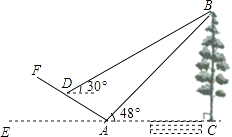
查看答案和解析>>
科目:初中数学 来源: 题型:
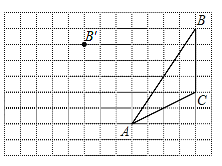
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为 1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B 的对应点 B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
(2)线段 AA′与线段 BB′的数量和位置关系是___________;
(3)求△A′B′C′的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com