
 如图,已知E,F是正方形ABCD的边BC和CD上的两点,且AE=AF,那么,当AB=4时,△AEF的面积S是CE的长x的函数吗?如果是,写出它的表达式,并回答x取何值时,△AEF的面积是最大的,求出此时△AEF的面积与正方形ABCD的面积之比.
如图,已知E,F是正方形ABCD的边BC和CD上的两点,且AE=AF,那么,当AB=4时,△AEF的面积S是CE的长x的函数吗?如果是,写出它的表达式,并回答x取何值时,△AEF的面积是最大的,求出此时△AEF的面积与正方形ABCD的面积之比. 分析 由已知可得,AB=BC=CD=AD=4,CE=x,由图形得出y=SABCD-S△ABE-S△ADF-S△CEF,便可求出x与S的关系式.
解答 解:(1)在Rt△ABE和Rt△ADF中,∵AB=AD,AE=AF,
∴Rt△ABE≌Rt△ADF,
∴BE=DF=4-x,
∴y=SABCD-S△ABE-S△ADF-S△CEF,
S=42-$\frac{1}{2}$×4×(4-x)-$\frac{1}{2}$×4(4--x)-$\frac{1}{2}$x2
S=-$\frac{1}{2}$x2+4x(0<x≤4),
当AB=4时,△AEF的面积S是CE的长x的函数.
S=-$\frac{1}{2}$x2+4x=-$\frac{1}{2}$(x-4)2+8
当x=4时,S最大=8,
△AEF的面积与正方形ABCD的面积之比是8:16=1:2.
点评 本题考查了二次函数的应用,利用面积的和差得出二次函数是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
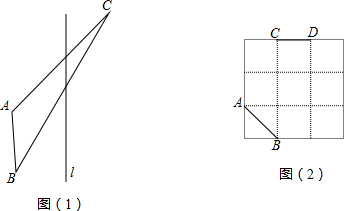
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
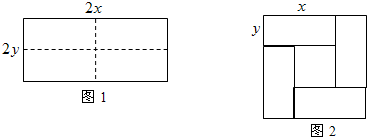
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
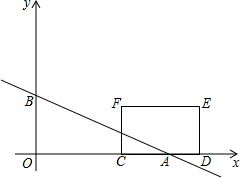 如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{3}$x+b(b>0),分别交x轴、y轴于A、B两点,点C(3,0),D(6,0),以CD为一边在x轴上方作矩形CDEF,CF=$\sqrt{3}$,设矩形CDEF与△ABO重叠部分的面积为S.
如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{3}$x+b(b>0),分别交x轴、y轴于A、B两点,点C(3,0),D(6,0),以CD为一边在x轴上方作矩形CDEF,CF=$\sqrt{3}$,设矩形CDEF与△ABO重叠部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
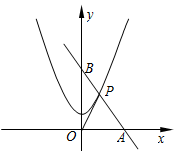 已知,如图,直线AB经过点B(0,6),且tan∠ABO=$\frac{2}{3}$,与抛物线y=ax2+2在第一象限内相交于点P,又知△AOP的面积为6.
已知,如图,直线AB经过点B(0,6),且tan∠ABO=$\frac{2}{3}$,与抛物线y=ax2+2在第一象限内相交于点P,又知△AOP的面积为6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com