
 如图所示,在?ABCD中,AC与BD交于点O,EG⊥FH于点O.求证:四边形EFGH为菱形.
如图所示,在?ABCD中,AC与BD交于点O,EG⊥FH于点O.求证:四边形EFGH为菱形.
|


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
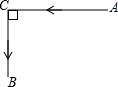 甲船和乙船分别从A港和C港同时出发,各沿图中箭头所指的方向航行(如图所示).现已知甲、乙两船的速度分别是16海里/时和12海里/时,且A,C两港之间的距离为10海里.问:经过多长时间,甲船和乙船之间的距离最短?最短距离为多少?(注:题中的“距离”都指直线距离,图中AC⊥CB.)
甲船和乙船分别从A港和C港同时出发,各沿图中箭头所指的方向航行(如图所示).现已知甲、乙两船的速度分别是16海里/时和12海里/时,且A,C两港之间的距离为10海里.问:经过多长时间,甲船和乙船之间的距离最短?最短距离为多少?(注:题中的“距离”都指直线距离,图中AC⊥CB.)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
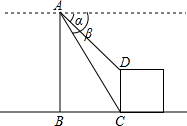 关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ;
关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ;| tanα+tanβ |
| 1-tanα•tanβ |
| tan45°+tan60° |
| 1-tan45°•tan60° |
1+
| ||
1-1×
|
(1+
| ||||
(1-
|
4+2
| ||
| -2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com