Question

△ABC的三边长分别为a，b，c，且满足条件：a²c²-b²c²=a⁴-b⁴，试判断△ABC的形状.

解：∵ ，-------------------①

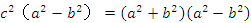∴ .----------②

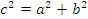∴ .---------------------------------------③

∴ △ABC为直角三角形.-------------------------- ④

上述解答过程中，第_______步开始出现错误，应改正为__________________________，

正确答案：△ABC是____________________________________.

 

Answer 1

【答案】

③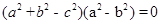，，等腰三角形或直角三角形．

【解析】

试题分析：把式子a²c²-b²c²=a⁴-b⁴变形化简后判定则可．如果三角形有两边的平方和等于第三边的平方，那么这个是直角三角形判定则可．如果没有这种关系，这个就不是直角三角形．

试题解析：：∵a²c²-b²c²=a⁴-b⁴，

∴（a²c²-b²c²）-（a⁴-b⁴）=0，

∴c²（a+b）（a-b）-（a+b）（a-b）（a²+b²）=0，

∴（a+b）（a-b）（c²-a²-b²）=0，

∵a+b≠0，

∴a-b=0或c²-a²-b²=0，

所以a=b或c²=a²+b²即它是等腰三角形或直角三角形．

考点: 1.因式分解；2.等腰直角三角形的判定.