
 如图,已知两条射线PQ∥MN,线段AB的两个端点A、B分别在射线PQ、MN上,且∠M=∠ABM=72°,D在线段MB上(点D不与M、B重合),PB平分∠APD,PC平分∠MPD.
如图,已知两条射线PQ∥MN,线段AB的两个端点A、B分别在射线PQ、MN上,且∠M=∠ABM=72°,D在线段MB上(点D不与M、B重合),PB平分∠APD,PC平分∠MPD.分析 (1)根据平行线的性质得∠MPA=180°-∠M=108°,再利用角平分线的定义得到∠1=∠2,∠3=∠4,然后根据三角形外角性质可求出∠BPC的度数;
(2)由PQ∥MN得到∠5=∠1,则∠2=∠5,再利用三角形外角性质得到∠6=∠2+∠5,所以∠6=2∠5;
(3)由三角形外角性质得∠PCM=∠BPC+∠5=54°+∠5,加上∠ABP=72°-∠5,若∠ABP<$\frac{1}{2}$∠PCM,则72°-∠5<$\frac{1}{2}$(54°+∠5),可解得∠5>30°,于是可判断当30°<∠PBM<72°时,∠ABP<$\frac{1}{2}$<∠PCM.
解答 解:(1)∵PQ∥MN,
∴∠MPA=180°-∠M=180°-72°=108°,
∵PB平分∠APD,PC平分∠MPD,
∴∠1=∠2,∠3=∠4,
∴∠2+∠3=$\frac{1}{2}∠$APD+$\frac{1}{2}∠$MPD=$\frac{1}{2}∠$MPA=54°,
即∠BPC=54°;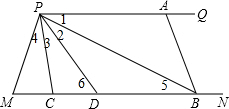
(2)不变.
∵PQ∥MN,
∴∠5=∠1,
∵∠1=∠2,
∴∠2=∠5,
∵∠6=∠2+∠5,
∴∠6=2∠5,
∴$\frac{∠PBM}{∠PDM}$=$\frac{1}{2}$;
(3)存在.
∵∠PCM=∠BPC+∠5=54°+∠5,
∠ABP=72°-∠5,
而∠ABP<$\frac{1}{2}$∠PCM,
∴72°-∠5<$\frac{1}{2}$(54°+∠5),
∴∠5>30°,
即在平行移动线段AB的过程中,当30°<∠PBM<72°时,∠ABP<$\frac{1}{2}$<∠PCM.
点评 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.也考查了平行线的性质和三角形外角性质.


科目:初中数学 来源: 题型:选择题
| A. | 一只手掌心大 | B. | 一本数学课本大 | C. | 一张教师讲台大 | D. | 一个教室大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<-$\frac{4}{3}$ | B. | x≥$\frac{4}{3}$ | C. | x<$\frac{4}{3}$ | D. | x≤-$\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若AC=9cm,DE=4cm,则AE的长度为( )
如图,△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若AC=9cm,DE=4cm,则AE的长度为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 110° | B. | 105° | C. | 90° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 37 | B. | 58 | C. | 89 | D. | 145 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com