
【题目】如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA:PC的值.
(3)在(2)的条件下,已知AB=3,OB:BP=3:1,求四边形AOCP的面积.

【答案】(1)、PA=2;(2)、1:1;(3)、16.
【解析】
试题分析:(1)、根据点P与点B重合,得出PA的长度;(2)、过点P作PM⊥x轴,过点P作PN⊥y轴,根据点A的纵坐标和点B的横坐标相等得出OA=OB,根据∠OAB=90°可得∠AOB=∠ABO=45°,结合角度之间的关系得出△ANP和△CMP全等得出PA=PC,从而得到比值;(3)、根据∠ANP=∠MON=∠OMP =90°得出四边形OMPN为矩形,根据PM=PN得出四边形OMPN为正方形,根据OA=AB=3,得出OB、BP、OP的长度,根据△ANP和△CMP全等得出四边形的面积.
试题解析:(1)、∵点P与点B重合,点B的坐标是(2,1), ∴点P的坐标是(2,1). ∴PA的长为2
(2)、过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,如图1所示

∵点A的纵坐标与点B的横坐标相等, ∴OA=AB. ∵∠OAB=90°,
∴∠AOB=∠ABO=45° ∵∠AOC=90°, ∴∠POC=45° ∵PM⊥x轴,PN⊥y轴,
∴PM=PN,∠ANP=∠CMP=∠OMP =90° ∴∠NPM=90° ∵∠APC=90° ∴∠APN=90°﹣∠APM=∠CPM
在△ANP和△CMP中, ∵∠APN=∠CPM,PN=PM,∠ANP=∠CMP, ∴△ANP≌△CMP.
∴PA=PC. ∴PA:PC的值为1:1
(3)、∵∠ANP=∠MON=∠OMP =90° ∴四边形OMPN为矩形 ∵PM=PN ∴四边形OMPN为正方形
∵∠OAB=90°,OA=AB=3 ∴OB=![]() ∵OB:BP=3:1 ∴BP=
∵OB:BP=3:1 ∴BP=![]() ∴OP=
∴OP=![]()
∴![]() 正方形OMPN=
正方形OMPN= ∵△ANP≌△CMP. ∴S△ANP≌S△CMP. ∴
∵△ANP≌△CMP. ∴S△ANP≌S△CMP. ∴![]() 四边形AOCO=
四边形AOCO=![]() 正方形OMPN=16
正方形OMPN=16


科目:初中数学 来源: 题型:
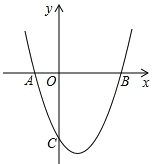
【题目】如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.
(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )

A.6 B.7 C.8 D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“神州五号”载人飞船绕地球飞行14圈,共飞行590200km,这个飞行距离用科学计数法表示为( )
A. 59.02×104km B. 0.5902×106km C. 5.902×105km D. 5.902×104km
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com